题目内容
【题目】已知椭圆C: ![]() (a>b>0)的左、右焦点分别为F1、F2 , 离心率e=
(a>b>0)的左、右焦点分别为F1、F2 , 离心率e= ![]() ,与双曲线
,与双曲线 ![]() 有相同的焦点. (I)求椭圆C的标准方程;
有相同的焦点. (I)求椭圆C的标准方程;
(II)过点F1的直线l与该椭圆C交于M、N两点,且| ![]() +
+ ![]() N|=
N|= ![]() ,求直线l的方程.
,求直线l的方程.
(Ⅲ)是否存在圆心在原点的圆,使得该圆的任一条切线与椭圆C有两个交点A、B,且OA⊥OB?若存在,写出该圆的方程,否则,说明理由.
【答案】解:(Ⅰ)由双曲线 ![]() ,得
,得 ![]() ,c=1, 又
,c=1, 又 ![]() ,得a=
,得a= ![]() ,∴b2=1,
,∴b2=1,
故椭圆C的标准方程为 ![]() ;
;
(Ⅱ)由(Ⅰ)得F1(﹣1,0),设过点F1(﹣1,0)的直线l:y=k(x+1),
由 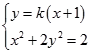 消去y,得(1+2k2)x2+4k2x+2k2﹣2=0,
消去y,得(1+2k2)x2+4k2x+2k2﹣2=0,
设M(x1 . y1),N(x2 , y2),
则x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
y1+y2=k(x1+x2+2)= ![]() ,
,
由于F2(1,0),| ![]() +
+ ![]() N|=
N|= ![]() ,
,
则 ![]() =(x1﹣1,y1),
=(x1﹣1,y1), ![]() =(x2﹣1,y2),
=(x2﹣1,y2),
即有(x1+x2﹣2)2+(y1+y2)2= ![]() ,
,
即有(﹣ ![]() ﹣2)2+(
﹣2)2+( ![]() )2=
)2= ![]() ,
,
解得k2=1.检验:△=16k4﹣4(1+2k2)((2k2﹣2)=16>0,
故k=±1.
则直线l的方程为:y=x+1或y=﹣x﹣1;
(Ⅲ)假设存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点
A(x1 , y1),B(x2 , y2)且OA⊥OB,
①当圆的切线不垂直x轴时,设该圆的切线方程为y=kx+m,
与x2+2y2=2联立得(1+2k2)x2+4kmx+2m2﹣2=0,
∴△=8(2k2﹣m2+1)>0,
∴ ![]() ,
,
∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2= ![]() ,
,
∵ ![]() =x1x2+y1y2=0,
=x1x2+y1y2=0,
∴ ![]() ,
,
∴3m2﹣2k2﹣2=0,则2k2=3m2﹣2,
∴对任意k,符合条件的m满足  ,
,
∴ ![]() ,即m≥
,即m≥ ![]() 或m≤﹣
或m≤﹣ ![]() ,
,
∵直线y=kx+m为圆心在原点的圆的一条切线,
∴圆的半径为r= ![]() ,
, ![]() =
= 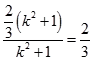 ,
,
∴所求的圆为 ![]() ,此时该圆的切线y=kx+m都满足m≥
,此时该圆的切线y=kx+m都满足m≥ ![]() 或m≤﹣
或m≤﹣ ![]() ,
,
∴所求的圆为 ![]() ,
,
②当切线的斜率不存在时,切线x=± ![]() ,
,
与椭圆x2+2y2=2的两个交点为( ![]() ,±
,± ![]() )或(﹣
)或(﹣ ![]() ,±
,± ![]() ),
),
满足OA⊥OB,
综上,存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1 , y1),B(x2 , y2)且OA⊥OB
【解析】(I)由双曲线方程求出椭圆的焦点,结合离心率求得a,b的值,则椭圆方程可求;(II)设出过F1的直线l的方程,与椭圆方程联立,由向量的模列式求得直线的斜率得答案;(Ⅲ)假设存在圆心在原点的圆使圆的任意一条切线与椭圆E恒有两个交点A(x1 , y1),B(x2 , y2)且OA⊥OB,然后分当圆的切线不垂直x轴时,设该圆的切线方程为y=kx+m,与x2+2y2=2联立得(1+2k2)x2+4kmx+2m2﹣2=0,利用向量垂直与数量积间的关系求得直线方程,已知切线垂直x轴时得答案.