题目内容
【题目】我国是世界上严重缺水的国家之一，城市缺水问题较为突出.某市为了节约生活用水，计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准03.5，用水量不超过a的部分按照平价收费，超过a的部分按照议价收费).为了较为合理地确定出这个标准，通过抽样获得了 100位居民某年的月均用水量(单位:t)，制作了频率分布直方图.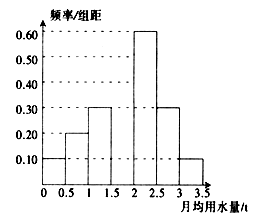
（1）由于某种原因频率分布直方图部分数据丢失，请在图中将其补充完整；
（2）用样本估计总体，如果希望80%的居民每月的用水量不超出标准03.5，则月均用水量的最低标准定为多少吨，请说明理由；
（3）从频率分布直方图中估计该100位居民月均用水量的平均数（同一组中的数据用该区间的中点值代表).
【答案】
（1）解：如图
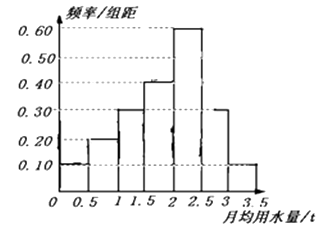
（2）解：月均用水量的最低标准应定为2.5吨.样本中月均用水量不低于2.5吨的居民有20位，占样本总体的 
，由样本估计总体，要保证80%的居民每月的用水量不超出标准，月均用水量的最低标准应定为2.5吨
（3）解：这100为居民的月均用水量的平均数为：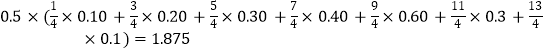 
【解析】(1)根据题意结合图像补全频率分布直方图即可。(2)由样本估计总体作出解释即可。(3)找出居民用水量的众数、中位数，求出平均值即可。
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识，掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息，以及对用样本的频率分布估计总体分布的理解，了解样本数据的频率分布表和频率分布直方图，是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律，它可以让我们更清楚的看到整个样本数据的频率分布情况，并由此估计总体的分布情况．
