题目内容
下列说法错误的是( )A.命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”
B.“x=1”是“x2-3x+2=0”的充分不必要条件
C.直线l与平面α垂直的充分必要条件是l与平面α内的两条直线垂直
D.命题p:?x∈R使得x2+x+1<0,则非p:?x∈R均有x2+x+1≥0
【答案】分析:本题考查的是命题的真假判断与应用问题.在解答时,应结合选项逐一判断:对A根据写逆否命题的规律:将条件结论互换并且取否定即可获得问题的解答;
对B根据方程与根的关系即可获得问题的解答;对C结合线面垂直的判定定理即可获得问题的解答;对D结合不等式及函数与方程的思想即可获得问题的解答.
解答:解:对A、根据写逆否命题的规律:将条件结论互换并且取否定,则命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”正确;
对B、根据方程与根的关系可知,若x=1则x2-3x+2=1-3+2=0,∴x2-3x+2=0成立,而若x2-3x+2=0成立则x=1或x=2.所以“x=1”是“x2-3x+2=0”的充分不必要条件正确;
对C、因为若直线l与平面α垂直则l与平面α内的两条直线垂直成立,若l与平面α内的两条直线垂直成立,则根据线面垂直的判定定理可知直线l与平面α垂直不一定成立.
故直线l与平面α垂直的充分必要条件是l与平面α内的两条直线垂直错误;
对D、根据特称命题的否定可知命题p:?x∈R使得x2+x+1<0,则非p:?x∈R均有x2+x+1≥0成立.
故选C.
点评:本题考查的是命题的真假判断与应用问题.在解答的过程当中充分体现了原命题与逆否命题的关系、方程与根的关系、线面垂直的判定问题以及函数与方程的思想.值得同学们体会和反思.
对B根据方程与根的关系即可获得问题的解答;对C结合线面垂直的判定定理即可获得问题的解答;对D结合不等式及函数与方程的思想即可获得问题的解答.
解答:解:对A、根据写逆否命题的规律:将条件结论互换并且取否定,则命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”正确;
对B、根据方程与根的关系可知,若x=1则x2-3x+2=1-3+2=0,∴x2-3x+2=0成立,而若x2-3x+2=0成立则x=1或x=2.所以“x=1”是“x2-3x+2=0”的充分不必要条件正确;
对C、因为若直线l与平面α垂直则l与平面α内的两条直线垂直成立,若l与平面α内的两条直线垂直成立,则根据线面垂直的判定定理可知直线l与平面α垂直不一定成立.
故直线l与平面α垂直的充分必要条件是l与平面α内的两条直线垂直错误;
对D、根据特称命题的否定可知命题p:?x∈R使得x2+x+1<0,则非p:?x∈R均有x2+x+1≥0成立.
故选C.
点评:本题考查的是命题的真假判断与应用问题.在解答的过程当中充分体现了原命题与逆否命题的关系、方程与根的关系、线面垂直的判定问题以及函数与方程的思想.值得同学们体会和反思.

练习册系列答案
相关题目
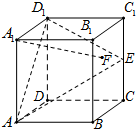 在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,记A1F与平面BCC1B1所成的角为θ,下列说法错误的是( )
在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,记A1F与平面BCC1B1所成的角为θ,下列说法错误的是( )| A、点F的轨迹是一条线段 | ||
| B、A1F与D1E不可能平行 | ||
| C、A1F与BE是异面直线 | ||
D、tanθ≤2
|
 如图,在平行四边形ABCD中,O是对角线AC,BD的交点,N是线段OD的中点,AN的延长线与CD交于点E,则下列说法错误的是( )
如图,在平行四边形ABCD中,O是对角线AC,BD的交点,N是线段OD的中点,AN的延长线与CD交于点E,则下列说法错误的是( )