题目内容
已知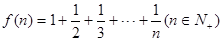 .经计算得
.经计算得 ,
, ,
, ,
, ,
, ,通过观察,我们可以得到一个一般性的结论.
,通过观察,我们可以得到一个一般性的结论.
(1)试写出这个一般性的结论;
(2)请用数学归纳法证明这个一般性的结论;
(3)对任一给定的正整数 ,试问是否存在正整数
,试问是否存在正整数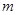 ,使得
,使得 ?
?
若存在,请给出符合条件的正整数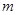 的一个值;若不存在,请说明理由.
的一个值;若不存在,请说明理由.
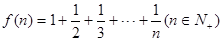 .经计算得
.经计算得 ,
, ,
, ,
, ,
, ,通过观察,我们可以得到一个一般性的结论.
,通过观察,我们可以得到一个一般性的结论. (1)试写出这个一般性的结论;
(2)请用数学归纳法证明这个一般性的结论;
(3)对任一给定的正整数
 ,试问是否存在正整数
,试问是否存在正整数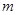 ,使得
,使得 ?
?若存在,请给出符合条件的正整数
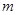 的一个值;若不存在,请说明理由.
的一个值;若不存在,请说明理由.见解析
(1)观察规律2,4,8,16,…, ;
; ,所以
,所以 .
.
(2)用数学归纳法证明时要分两个步骤:一是先验证:当n=1时,不等式成立;二是先假设n=k时,不等式成立,再证明当n=k+1时,命题也成立,但一定要用上n=k时的归纳假设.
(3)令 ,当n=2a时,
,当n=2a时, 符合要求.所在存在
符合要求.所在存在
(1) (当且仅当
(当且仅当 时取等号)………4分
时取等号)………4分
(2)证明:(数学归纳法)
 当
当 时,显然成立
时,显然成立
 假设当
假设当 时成立,即
时成立,即 ……………………6分
……………………6分
当 时,左边
时,左边



 右边
右边
即当 时,也成立.………………………10分
时,也成立.………………………10分
由
 知,
知, 成立.…………………………12分
成立.…………………………12分
(3)存在……………………………………13分
可取 ……………………………16分
……………………………16分
注:答案不唯一
 ;
; ,所以
,所以 .
.(2)用数学归纳法证明时要分两个步骤:一是先验证:当n=1时,不等式成立;二是先假设n=k时,不等式成立,再证明当n=k+1时,命题也成立,但一定要用上n=k时的归纳假设.
(3)令
 ,当n=2a时,
,当n=2a时, 符合要求.所在存在
符合要求.所在存在(1)
 (当且仅当
(当且仅当 时取等号)………4分
时取等号)………4分(2)证明:(数学归纳法)
 当
当 时,显然成立
时,显然成立 假设当
假设当 时成立,即
时成立,即 ……………………6分
……………………6分当
 时,左边
时,左边



 右边
右边即当
 时,也成立.………………………10分
时,也成立.………………………10分由

 知,
知, 成立.…………………………12分
成立.…………………………12分(3)存在……………………………………13分
可取
 ……………………………16分
……………………………16分注:答案不唯一

练习册系列答案
相关题目

 ,那么
,那么 ,
, ,
, 中至少有一个不小于
中至少有一个不小于 ”时,反设正确的是( )
”时,反设正确的是( ) <
<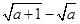 ,其中a≥0.=
,其中a≥0.=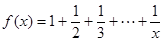 ,计算得当
,计算得当 时
时 ,当
,当 时有
时有 ,
, ,
, ,
, ,因此猜测当
,因此猜测当 ,
, ,
, 中至少有一个不小于2”时的假设为_ _____
中至少有一个不小于2”时的假设为_ _____  若
若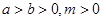 ,则
,则 与
与 的关系( )
的关系( ) ,求证:
,求证: ,用反证法证明时,可假设
,用反证法证明时,可假设 ;
; ,
, ,求证:方程
,求证:方程 的两根的绝对值都小于1.用反证法证明时可假设方程有一根
的两根的绝对值都小于1.用反证法证明时可假设方程有一根 的绝对值大于或等于1,即假设
的绝对值大于或等于1,即假设 ,以下结论正确的是( )
,以下结论正确的是( ) 与
与 的假设都错误
的假设都错误 没有最小数”时,可用反证法证明.
没有最小数”时,可用反证法证明. 是
是 中的最小数,则取
中的最小数,则取 ,可得:
,可得: ,与假设中“
,与假设中“ 是
是 没有最大数”,也可以用反证法证明.我们可以假设
没有最大数”,也可以用反证法证明.我们可以假设 是
是 中的最大数,则可以找到
中的最大数,则可以找到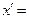 ▲ (用
▲ (用 ,
, 表示),由此可知
表示),由此可知 ,
, ,这与假设矛盾!所以数集
,这与假设矛盾!所以数集