题目内容
 已知椭圆
已知椭圆| x2 |
| 16 |
| y2 |
| 12 |
(1)当P点在椭圆上运动时,求R形成的轨迹方程;
(2)设点R形成的曲线为C,直线l:y=k(x+4
| 2 |
分析:(1)F1(-2,0),F2(2,0)设R(x,y),Q(x1,y1).由|PQ|=|PF2|,知|F1Q|=|F2P|+|PQ|=|F1P|+|PF2|=8,所以(x1+2)2+y12=64,由此能导出R的轨迹方程.
(2)当∠AOB=90°时,在Rt△AOC中,∠AOC=45°,此时弦心距|OC|=2
,又|OC|=
.由此能导出k的值.
(2)当∠AOB=90°时,在Rt△AOC中,∠AOC=45°,此时弦心距|OC|=2
| 2 |
|4
| ||
|
解答: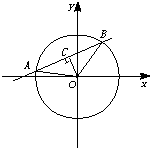 解:(1)F1(-2,0),F2(2,0)设R(x,y),Q(x1,y1).∵|PQ|=|PF2|,
解:(1)F1(-2,0),F2(2,0)设R(x,y),Q(x1,y1).∵|PQ|=|PF2|,
∴|F1Q|=|F2P|+|PQ|=|F1P|+|PF2|=8,则(x1+2)2+y12=64.(4分)
又
得x1=2x-2,y1=2y.
∴(2x)2+(2y)2=64,故R的轨迹方程为:x2+y2=16(7分)
(2)如图,当∠AOB=90°时,
在Rt△AOC中,∠AOC=45°,此时弦心距|OC|=2
又|OC|=
.由
=2
得k=±
.(12分)
 解:(1)F1(-2,0),F2(2,0)设R(x,y),Q(x1,y1).∵|PQ|=|PF2|,
解:(1)F1(-2,0),F2(2,0)设R(x,y),Q(x1,y1).∵|PQ|=|PF2|,∴|F1Q|=|F2P|+|PQ|=|F1P|+|PF2|=8,则(x1+2)2+y12=64.(4分)
又
|
∴(2x)2+(2y)2=64,故R的轨迹方程为:x2+y2=16(7分)
(2)如图,当∠AOB=90°时,
在Rt△AOC中,∠AOC=45°,此时弦心距|OC|=2
| 2 |
又|OC|=
|4
| ||
|
|4
| ||
|
| 2 |
| ||
| 3 |
点评:本题考查直线和圆锥曲线的位置关系的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知椭圆
已知椭圆