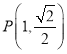Question

【题目】已知直线（）.

（1）求直线经过的定点坐标；

（2）若直线交负半轴于，交轴正半轴于，为坐标系原点，的面积为，求的最小值并求此时直线的方程.

Answer 1

【答案】（1）（2）S最小为4，直线

【解析】

试题分析：（1）由kx-y+1+2k=0，得y-1=k（x+2），显然过定点（-2，1）.（2）先求出A和B 的坐标，代入三角形的面积公式进行化简，再利用基本不等式求出三角形面积的最小值，以及面积最小时直线的斜率，从而得到直线l的方程

试题解析：（1）直线化为.

因为该式子对于任意的实数都成立，所以，解得.

所以直线过定点.

（2）时，；

当时，.

因为直线交负半轴于，交轴正半轴于，所以.

所以，

当且仅当，即时（舍去），等号成立，

此时直线的方程为，即.