题目内容
已知实数x、y满足:
则z=|x+2y-4|的最大值( )
|
分析:由实数x、y满足:
,作出可行域,利用角点法能求出z=|x+2y-4|的最大值.
|
解答:解:由实数x、y满足:
,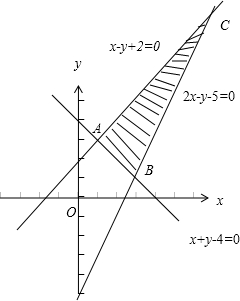
作出可行域:
∵z=|x+2y-4|,
解方程组
,得A(1,3),
∴ZA=|1+2×3-4|=3;
解方程组
,得B(3,1),
∴ZB=|3+2×1-4|=1;
解方程组
,得C(7,9),
∴ZC=|7+2×9-4|=21.
∴z=|x+2y-4|的最大值为21.
故选D.
|

作出可行域:
∵z=|x+2y-4|,
解方程组
|
∴ZA=|1+2×3-4|=3;
解方程组
|
∴ZB=|3+2×1-4|=1;
解方程组
|
∴ZC=|7+2×9-4|=21.
∴z=|x+2y-4|的最大值为21.
故选D.
点评:本题考查线性规划的求法,解题时要认真审题,注意角点法的合理运用.

练习册系列答案
相关题目