题目内容
已知曲线 :
:
 .
.
(1)若曲线 是焦点在
是焦点在 轴上的椭圆,求
轴上的椭圆,求 的取值范围;
的取值范围;
(2)设 ,过点
,过点 的直线
的直线 与曲线
与曲线 交于
交于 ,
, 两点,
两点, 为坐标原点,若
为坐标原点,若 为直角,求直线
为直角,求直线 的斜率.
的斜率.
 :
:
 .
.(1)若曲线
 是焦点在
是焦点在 轴上的椭圆,求
轴上的椭圆,求 的取值范围;
的取值范围;(2)设
 ,过点
,过点 的直线
的直线 与曲线
与曲线 交于
交于 ,
, 两点,
两点, 为坐标原点,若
为坐标原点,若 为直角,求直线
为直角,求直线 的斜率.
的斜率.(1) ;(2)
;(2) 的值为
的值为 .
.
 ;(2)
;(2) 的值为
的值为 .
.试题分析:(1)曲线
 是焦点在
是焦点在 轴上的椭圆,则求解不等式组
轴上的椭圆,则求解不等式组 即可得到参数
即可得到参数 的取值范围;(2)设
的取值范围;(2)设 的方程为
的方程为 (注意检验斜率不存在的情况是否符合要求),再设出
(注意检验斜率不存在的情况是否符合要求),再设出 两点的坐标
两点的坐标 ,当
,当 ,由
,由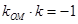 即
即 与
与 联立可求解出点
联立可求解出点 的坐标,然后再代入直线方程
的坐标,然后再代入直线方程 ,即可求出
,即可求出 的值.
的值.试题解析:(1)若曲线
 :
: 是焦点在
是焦点在 轴上的椭圆,则有
轴上的椭圆,则有
解得
 3分
3分(2)
 时,曲线
时,曲线 的方程为
的方程为 ,
, 为椭圆
为椭圆由题意知,点
 的直线
的直线 的斜率存在,所以设
的斜率存在,所以设 的方程为
的方程为
由
 消去
消去 得
得 5分
5分 ,当
,当 时,解得
时,解得
设
 两点的坐标分别为
两点的坐标分别为
因为
 为直角,所以
为直角,所以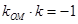 ,即
,即
整理得
 ① 7分
① 7分又
 ,②将①代入②,消去
,②将①代入②,消去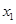 得
得
解得
 或
或 (舍去)
(舍去)将
 代入①,得
代入①,得 ,所以
,所以
故所求
 的值为
的值为 9分.
9分.
练习册系列答案
相关题目
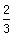 ,且过点
,且过点 ,点A、B分别是椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
,点A、B分别是椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于 轴上方,
轴上方, .
.
 的最小值.
的最小值. 分别是椭圆
分别是椭圆 的左、右焦点, 点
的左、右焦点, 点 在椭圆上
在椭圆上 上.
上. 若
若 、
、 均与椭圆
均与椭圆 轴上是否存在定点
轴上是否存在定点 ,点
,点 的距离之积恒为1?若存在,请求出点
的距离之积恒为1?若存在,请求出点 :
: ,直线
,直线 交椭圆
交椭圆 两点.
两点.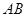 为直径的圆的方程.
为直径的圆的方程. 
 的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形. ,直线AM、BM相交于点M,且这两条直线的斜率之积为
,直线AM、BM相交于点M,且这两条直线的斜率之积为 .
. (
( )相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.
)相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R. 的直线与曲线M相交于A、B两点. 问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由.
的直线与曲线M相交于A、B两点. 问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由. 左焦点
左焦点 且倾斜角为
且倾斜角为 的直线交双曲线右支于点
的直线交双曲线右支于点 ,若线段
,若线段 的中点
的中点 落在
落在 轴上,则此双曲线的离心率为( )
轴上,则此双曲线的离心率为( )



 的圆心为抛物线
的圆心为抛物线 的焦点,直线
的焦点,直线 与圆
与圆 相切,则该圆的方程为( )
相切,则该圆的方程为( )


