题目内容
过双曲线 左焦点
左焦点 且倾斜角为
且倾斜角为 的直线交双曲线右支于点
的直线交双曲线右支于点 ,若线段
,若线段 的中点
的中点 落在
落在 轴上,则此双曲线的离心率为( )
轴上,则此双曲线的离心率为( )
 左焦点
左焦点 且倾斜角为
且倾斜角为 的直线交双曲线右支于点
的直线交双曲线右支于点 ,若线段
,若线段 的中点
的中点 落在
落在 轴上,则此双曲线的离心率为( )
轴上,则此双曲线的离心率为( )A. | B. | C. | D. |
D
试题分析:因为线段
 的中点
的中点 落在
落在 轴上,故
轴上,故 点与原点的连线为
点与原点的连线为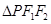 的中位线,则
的中位线,则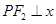 轴,故
轴,故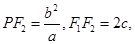
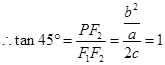 ,
,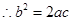 ,即
,即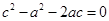 ,等式两边同除
,等式两边同除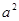 得
得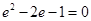 ,所以
,所以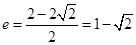 (舍去)或
(舍去)或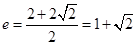 ,故选D.
,故选D.
练习册系列答案
相关题目
题目内容
 左焦点
左焦点 且倾斜角为
且倾斜角为 的直线交双曲线右支于点
的直线交双曲线右支于点 ,若线段
,若线段 的中点
的中点 落在
落在 轴上,则此双曲线的离心率为( )
轴上,则此双曲线的离心率为( )A. | B. | C. | D. |
 的中点
的中点 落在
落在 轴上,故
轴上,故 点与原点的连线为
点与原点的连线为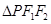 的中位线,则
的中位线,则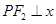 轴,故
轴,故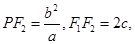
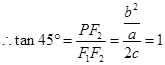 ,
,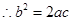 ,即
,即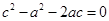 ,等式两边同除
,等式两边同除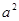 得
得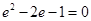 ,所以
,所以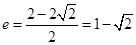 (舍去)或
(舍去)或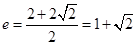 ,故选D.
,故选D.