题目内容
已知圆 的圆心为抛物线
的圆心为抛物线 的焦点,直线
的焦点,直线 与圆
与圆 相切,则该圆的方程为( )
相切,则该圆的方程为( )
 的圆心为抛物线
的圆心为抛物线 的焦点,直线
的焦点,直线 与圆
与圆 相切,则该圆的方程为( )
相切,则该圆的方程为( )A. | B. |
C. | D. |
B
试题分析:因为抛物线
 的焦点坐标为
的焦点坐标为 .又因为圆心的坐标为
.又因为圆心的坐标为 ,所以依题意可得
,所以依题意可得 .又因为直线
.又因为直线 与圆
与圆 相切,所以根据圆心到直线
相切,所以根据圆心到直线 的距离等于半径可得
的距离等于半径可得 .所圆的方程为
.所圆的方程为 .故选B.正确处理相切、抛物线的焦点坐标是关键.
.故选B.正确处理相切、抛物线的焦点坐标是关键.
练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
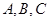 为椭圆
为椭圆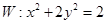 上的三个点,
上的三个点,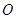 为坐标原点.
为坐标原点.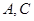 所在的直线方程为
所在的直线方程为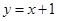 ,求
,求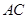 的长;
的长;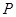 为线段
为线段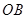 上一点,且
上一点,且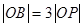 ,当
,当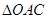 的面积是否为常数,并说明理由.
的面积是否为常数,并说明理由. :
:
 .
. 轴上的椭圆,求
轴上的椭圆,求 的取值范围;
的取值范围; ,过点
,过点 的直线
的直线 与曲线
与曲线 ,
, 两点,
两点, 为坐标原点,若
为坐标原点,若 为直角,求直线
为直角,求直线 :
: 的离心率为
的离心率为 且与双曲线
且与双曲线 :
: 有共同焦点.
有共同焦点.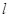 ,求
,求 ,过椭圆
,过椭圆 作
作 轴的垂线交
轴的垂线交 ,若
,若 点满足
点满足 ,
, ,连结
,连结 交
交 于点
于点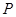 ,求证:
,求证: .
.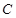 两焦点坐标分别为
两焦点坐标分别为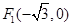 ,
,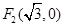 ,且经过点
,且经过点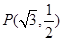 .
.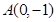 ,直线
,直线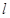 与椭圆
与椭圆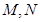 .若△
.若△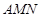 是以
是以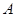 为直角顶点的等腰直角三角形,试求直线
为直角顶点的等腰直角三角形,试求直线 ,若椭圆C的一个焦点为F(
,若椭圆C的一个焦点为F( ,0),其短轴上的一个端点到F的距离为
,0),其短轴上的一个端点到F的距离为 .
. 且
且 =0,其中N为椭圆的下顶点,求直线在y轴上截距的取值范围.
=0,其中N为椭圆的下顶点,求直线在y轴上截距的取值范围. ,且经过点
,且经过点 ,直线
,直线 交椭圆于不同的两点A,B.
交椭圆于不同的两点A,B. 不过点M,求证:直线MA、MB与x轴围成一个等腰三角形
不过点M,求证:直线MA、MB与x轴围成一个等腰三角形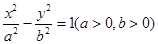 的顶点恰好是椭圆
的顶点恰好是椭圆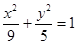 的两个顶点,且焦距是
的两个顶点,且焦距是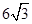 ,则此双曲线的渐近线方程是( )
,则此双曲线的渐近线方程是( )



 绕
绕 轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是 .
轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是 .