题目内容
3.若函数f(x)、g(x)在区间[-2,2]上是奇函数,则函数f(x)•g(x)在这个区间上是偶函数.(填写奇偶性)分析 利用奇偶函数的定义,即可得出结论.
解答 解:∵函数f(x)、g(x)在区间[-2,2]上是奇函数,
∴f(-x)=-f(x),g(-x)=-g(x),
∴f(-x)•g(-x)=[-f(x)]•[-g(x)]=f(x)•g(x),
∴f(x)•g(x)在这个区间上是偶函数.
故答案为:偶.
点评 本题考查函数的奇偶性,考查学生的计算能力,正确运用函数的奇偶性的定义是关键.

练习册系列答案
相关题目
18.函数y=($\frac{1}{4}$)${\;}^{{x}^{2}-x}$的值域为( )
| A. | (-∞,$\sqrt{2}$] | B. | (0,$\sqrt{2}$] | C. | [$\sqrt{3}$,+∞) | D. | (0,$\sqrt{3}$] |
15.等差数列{an}中,a4+a6=-6,S3=-27,则a9的值为( )
| A. | 3 | B. | 5 | C. | -4 | D. | -2 |
12.若f(x)=5-3x(2<x≤4),则f(x)的值域为( )
| A. | R | B. | [-7,-1) | C. | (-7,-1] | D. | {-7,-1} |
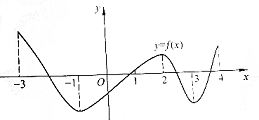 已知函数y=f(x)在区间[-3,4]上的图象如图所示,根据图象说出函数的单调区间,以及在每一个区间上函数的单调性.
已知函数y=f(x)在区间[-3,4]上的图象如图所示,根据图象说出函数的单调区间,以及在每一个区间上函数的单调性.