题目内容
【题目】如图,矩形![]() 和梯形
和梯形![]() 所在平面互相垂直,
所在平面互相垂直, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 的长为何值时,二面角
的长为何值时,二面角![]() 的大小为60°.
的大小为60°.
【答案】(1)见解析(2)![]()
【解析】试题分析:(I)由已知中在△BCE中,BC⊥CF,BC=AD=![]() ,BE=3,由勾股定理,我们易得EF⊥CE,由矩形ABCD和梯形BEFC所在平面互相垂直,可得DC⊥平面EFCB,则DC⊥EF,进而由线面垂直的判定定理得到答案.
,BE=3,由勾股定理,我们易得EF⊥CE,由矩形ABCD和梯形BEFC所在平面互相垂直,可得DC⊥平面EFCB,则DC⊥EF,进而由线面垂直的判定定理得到答案.
(II)以点C为坐标原点,以CB,CF和CD分别作为x轴,y轴和z轴,建立空间直角坐标系C﹣xyz,设AB=a,分别求出平面AEF的法向量和平面EFCB的法向量,代入向量夹角公式,由二面角A﹣EF﹣C的大小为60°,构造关于a的方程,解方程求出a值.
试题解析:
(1)证明:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() .又因为在
.又因为在![]() 中,
中,![]() ,所以
,所以![]() .
.
由已知条件知,![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]()
(2)如图,以点C为坐标原点,以CB,CF和CD分别作为x轴,y轴和z轴,建立空间直角坐标系C-xyz.
设AB=a(a >0),则C(0,0,0),A(![]() ,0,a),B(
,0,a),B(![]() ,0,0),E(
,0,0),E(![]() , 3,0),F(0,4,0).从而
, 3,0),F(0,4,0).从而![]()
设平面AEF的法向量为![]() ,由
,由![]() 得,
得,
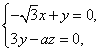 取x=1,则
取x=1,则![]() ,即
,即![]() .
.
不妨设平面EFCB的法向量为![]() ,
,
由条件,得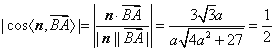 ,
,
解得![]() .所以当
.所以当![]() 时,二面角A-EF-C的大小为60°.
时,二面角A-EF-C的大小为60°.

【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪80元,每单抽成4元;乙公司无底薪,40单以内(含40单)的部分每单抽成6元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其50天的送餐单数,得到如下频数表:
甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 15 | 10 | 10 | 5 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 5 | 10 | 10 | 20 | 5 |
(1)现从甲公司记录的50天中随机抽取3天,求这3天送餐单数都不小于40的概率;
(2)若将频率视为概率,回答下列两个问题:
①记乙公司送餐员日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小王打算到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为小王作出选择,并说明理由.