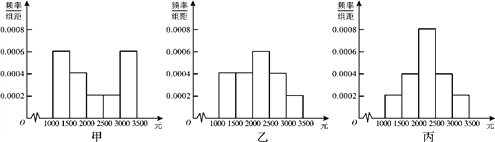
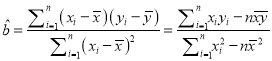题目内容
【题目】数列![]() 为递增的等比数列,
为递增的等比数列, ![]()
![]() ,
,
数列![]() 满足
满足![]() .
.
(Ⅰ)求数列![]() 的通项公式;(Ⅱ)求证:
的通项公式;(Ⅱ)求证: ![]() 是等差数列;
是等差数列;
(Ⅲ)设数列![]() 满足
满足![]() ,且数列
,且数列![]() 的前
的前![]() 项和
项和![]() ,并求使得
,并求使得![]() 对任意
对任意![]() 都成立的正整数
都成立的正整数![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]() 是首项为1,公差为2的等差数列. (3)4
是首项为1,公差为2的等差数列. (3)4
【解析】试题分析:(1)根据{an}为递增的等比数列且a32=a1a5,得到a1=1,a3=4,a5=16,进而求得an,bn的通项公式;(2)利用等差数列定义加以证明;(3)利用裂项相消法求数列的前n项和,再用分离参数法和单调性求m的最小值.
试题解析:
(1)数列![]() 为递增的等比数列,则其公比为正数,又
为递增的等比数列,则其公比为正数,又![]() ,当且仅当
,当且仅当![]() 时成立。此时公比
时成立。此时公比![]() 所以
所以![]() .
.
(2) 因为 ![]() ,所以
,所以![]() ,即
,即![]() .
.
所以![]() 是首项为
是首项为![]() ,公差为2的等差数列.
,公差为2的等差数列.
(3)![]() ,所以
,所以![]() .
.
![]() ,
,
![]()
![]() ,n∈N*,即数列{Tn}是递增数列.∴当n=1时,Tn取得最小值
,n∈N*,即数列{Tn}是递增数列.∴当n=1时,Tn取得最小值![]() ,
,
要使得![]() 对任意n∈N*都成立,结合(Ⅰ)的结果,只需
对任意n∈N*都成立,结合(Ⅰ)的结果,只需![]() ,
,
![]() ,故正整数m的最小值为4.
,故正整数m的最小值为4.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目