题目内容
如图,抛物线C1:y2=8x与双曲线 有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5.
有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5.(1)求双曲线C2的方程;
(2)以F1为圆心的圆M与双曲线的一条渐近线相切,圆N:(x-2)2+y2=1.已知点
 ,过点P作互相垂直且分别与圆M、圆N相交的直线l1和l2,设l1被圆M截得的弦长为s,l2被圆N截得的弦长为t.
,过点P作互相垂直且分别与圆M、圆N相交的直线l1和l2,设l1被圆M截得的弦长为s,l2被圆N截得的弦长为t. 是否为定值?请说明理由.
是否为定值?请说明理由.
【答案】分析:(1)根据抛物线C1的焦点为F2(2,0),得出双曲线C2的焦点为F1(-2,0)、F2(2,0),再设A(x,y)在抛物线C1上,根据|AF2|=5结合抛物线的定义得,x、y的值,最后根据双曲线定义结合点A在双曲线上,得a=1,可求双曲线方程;
(2)设圆M的方程为:(x+2)2+y2=r2,根据双曲线的渐近线方程和直线与圆相切的条件,得圆M的半径为 ,从而求出圆M的方程.过点P作互相垂直且分别与圆M、圆N相交的直线l1和l2,设其中的一条斜率为k,则另一条的斜率为
,从而求出圆M的方程.过点P作互相垂直且分别与圆M、圆N相交的直线l1和l2,设其中的一条斜率为k,则另一条的斜率为 ,利用直线的点斜式方程,将直线l1和l2的方程与圆M方程联解,可以得出弦长为s和t关于k的表达式,将其代入
,利用直线的点斜式方程,将直线l1和l2的方程与圆M方程联解,可以得出弦长为s和t关于k的表达式,将其代入 进行化简,可以得到定值
进行化简,可以得到定值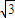 .
.
解答:解:(1)∵抛物线C1:y2=8x的焦点为F2(2,0),
∴双曲线C2的焦点为F1(-2,0)、F2(2,0),
设A(x,y)在抛物线C1:y2=8x上,且|AF2|=5,
由抛物线的定义得,x+2=5,∴x=3,∴y2=8×3,∴ ,
,
∴ ,
,
又∵点A在双曲线上,由双曲线定义得,2a=|7-5|=2,∴a=1,
∴双曲线的方程为: .
.
(2) 为定值.下面给出说明.
为定值.下面给出说明.
设圆M的方程为:(x+2)2+y2=r2,双曲线的渐近线方程为: ,
,
∵圆M与渐近线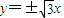 相切,∴圆M的半径为
相切,∴圆M的半径为 ,
,
故圆M:(x+2)2+y2=3,
显然当直线l1的斜率不存在时不符合题意,
设l1的方程为 ,即
,即 ,
,
设l2的方程为 ,即
,即 ,
,
∴点M到直线l1的距离为 ,点N到直线l2的距离为
,点N到直线l2的距离为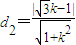 ,
,
∴直线l1被圆M截得的弦长 ,
,
直线l2被圆N截得的弦长 ,
,
∴ ,
,
故 为定值
为定值 .
.
点评:本题考查了圆方程、直线方程、圆锥曲线的基本量和圆与圆锥曲线的关系等知识点,属于难题.解决本题一方面要求对圆方程、直线方程、圆锥曲线的方程有熟悉的理解,另一方面要求对含有字母的代数式化简、计算要精确到位,具有较强的综合性.
(2)设圆M的方程为:(x+2)2+y2=r2,根据双曲线的渐近线方程和直线与圆相切的条件,得圆M的半径为
 ,从而求出圆M的方程.过点P作互相垂直且分别与圆M、圆N相交的直线l1和l2,设其中的一条斜率为k,则另一条的斜率为
,从而求出圆M的方程.过点P作互相垂直且分别与圆M、圆N相交的直线l1和l2,设其中的一条斜率为k,则另一条的斜率为 ,利用直线的点斜式方程,将直线l1和l2的方程与圆M方程联解,可以得出弦长为s和t关于k的表达式,将其代入
,利用直线的点斜式方程,将直线l1和l2的方程与圆M方程联解,可以得出弦长为s和t关于k的表达式,将其代入 进行化简,可以得到定值
进行化简,可以得到定值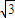 .
.解答:解:(1)∵抛物线C1:y2=8x的焦点为F2(2,0),
∴双曲线C2的焦点为F1(-2,0)、F2(2,0),
设A(x,y)在抛物线C1:y2=8x上,且|AF2|=5,
由抛物线的定义得,x+2=5,∴x=3,∴y2=8×3,∴
 ,
,∴
 ,
,又∵点A在双曲线上,由双曲线定义得,2a=|7-5|=2,∴a=1,
∴双曲线的方程为:
 .
.(2)
 为定值.下面给出说明.
为定值.下面给出说明.设圆M的方程为:(x+2)2+y2=r2,双曲线的渐近线方程为:
 ,
,∵圆M与渐近线
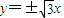 相切,∴圆M的半径为
相切,∴圆M的半径为 ,
,故圆M:(x+2)2+y2=3,
显然当直线l1的斜率不存在时不符合题意,
设l1的方程为
 ,即
,即 ,
,设l2的方程为
 ,即
,即 ,
,∴点M到直线l1的距离为
 ,点N到直线l2的距离为
,点N到直线l2的距离为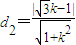 ,
,∴直线l1被圆M截得的弦长
 ,
,直线l2被圆N截得的弦长
 ,
,∴
 ,
,故
 为定值
为定值 .
.点评:本题考查了圆方程、直线方程、圆锥曲线的基本量和圆与圆锥曲线的关系等知识点,属于难题.解决本题一方面要求对圆方程、直线方程、圆锥曲线的方程有熟悉的理解,另一方面要求对含有字母的代数式化简、计算要精确到位,具有较强的综合性.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
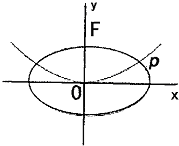 如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:
如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2: (2012•河北模拟)如图,抛物线C1:y2=2px(p>0)的焦点为F,A为C1上的点,以F为圆心,
(2012•河北模拟)如图,抛物线C1:y2=2px(p>0)的焦点为F,A为C1上的点,以F为圆心, 的离心率
的离心率 ,C1与C2在第一象限的交点为
,C1与C2在第一象限的交点为 ,
, 。
。 
 如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x,y)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x=1-
如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x,y)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x=1-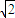 时,切线MA的斜率为-
时,切线MA的斜率为- .
. 如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x,y)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x=1-
如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x,y)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x=1- 时,切线MA的斜率为-
时,切线MA的斜率为- .
.