题目内容
 如图过抛物线C1:x2=4y的对称轴上一点P(0,m)(m>0)作直线l与抛物线交于A(x1,y1),B(x2,y2)两点,点Q是P关于原点的对称点,以P,Q为焦点的椭圆为C2.
如图过抛物线C1:x2=4y的对称轴上一点P(0,m)(m>0)作直线l与抛物线交于A(x1,y1),B(x2,y2)两点,点Q是P关于原点的对称点,以P,Q为焦点的椭圆为C2.(1)求证:x1x2为定值;
(2)若l的方程为x-2y+4=0,且C1,C2以及直线l有公共点,求C2的方程;
(3)设
| AP |
| PB |
| QP |
| QA |
| QB |
分析:(1)设直线l的方程为y=kx+m,联立
,得x2-4kx-4m=0,由此能够证明x1x2=-4m.
(2)由l的方程为x-2y+4=0,知m=2,由点Q是P关于原点的对称点,知P(0,2),Q(0,-2),联立
,得A(-2,1),B(4,4),由C1,C2以及直线l有公共点,知C1,C2以及直线l的公共点为A(-2,1),由此能求出椭圆为C2的方程.
(3)由
=λ
,知
=-λ,因为Q(0,-m),
=(x1,y1+m),
=(x2,y2+m)所以
-μ
=(x1-μx2,y1-μy2+(1-μ)m),由此能够证明λ=μ.
|
(2)由l的方程为x-2y+4=0,知m=2,由点Q是P关于原点的对称点,知P(0,2),Q(0,-2),联立
|
(3)由
| AP |
| PB |
| x1 |
| x2 |
| QA |
| QB |
| QA |
| QB |
解答:解:(1)设直线l的方程为y=kx+m,
联立
,得x2-4kx-4m=0,
∵直线l与抛物线交于A(x1,y1),B(x2,y2)两点,
∴x1x2=-4m.
(2)∵l的方程为x-2y+4=0,∴m=2,
∵点Q是P关于原点的对称点,
∴P(0,2),Q(0,-2),
联立
,得A(-2,1),B(4,4),
∵C1,C2以及直线l有公共点,
∴C1,C2以及直线l的公共点为A(-2,1),
∵P,Q为焦点的椭圆为C2,∴设椭圆为C2的方程为
+
=1.
由C1,C2以及直线l的公共点为A(-2,1),
知2a=
+
=
+
,
∴a2=
,
∴椭圆为C2的方程为
+
=1.
(3)由
=λ
,则
=-λ,
因为Q(0,-m),
=(x1,y1+m),
=(x2,y2+m)
所以
-μ
=(x1-μx2,y1-μy2+(1-μ)m),
=(0,2m),
⊥(
-μ
),
∴2m[y1-μy2+(1-μ)m]=0,
从而
-μ
+(1-μ)m=0,
即
-μ
+4(1-μ)m=0
-μ
-(1-μ)x1x2=0,
-μ
-(1-μ)=0,
故
=-μ或
=-1(舍去)
故λ=μ.
联立
|
∵直线l与抛物线交于A(x1,y1),B(x2,y2)两点,
∴x1x2=-4m.
(2)∵l的方程为x-2y+4=0,∴m=2,
∵点Q是P关于原点的对称点,
∴P(0,2),Q(0,-2),
联立
|
∵C1,C2以及直线l有公共点,
∴C1,C2以及直线l的公共点为A(-2,1),
∵P,Q为焦点的椭圆为C2,∴设椭圆为C2的方程为
| x2 |
| a2-4 |
| y2 |
| a2 |
由C1,C2以及直线l的公共点为A(-2,1),
知2a=
| 4+1 |
| 4+9 |
| 5 |
| 13 |
∴a2=
18+2
| ||
| 4 |
∴椭圆为C2的方程为
| 2x2 | ||
1+
|
| 2y2 | ||
9+
|
(3)由
| AP |
| PB |
| x1 |
| x2 |
因为Q(0,-m),
| QA |
| QB |
所以
| QA |
| QB |
| QP |
| QP |
| QA |
| QB |
∴2m[y1-μy2+(1-μ)m]=0,
从而
| ||
| 4 |
| ||
| 4 |
即
| x | 2 1 |
| x | 2 2 |
| x | 2 1 |
| x | 2 2 |
| x1 |
| x2 |
| x2 |
| x1 |
故
| x1 |
| x2 |
| x1 |
| x2 |
故λ=μ.
点评:本题考查x1x2为定值的证明,求椭圆C2的方程和求证:λ=μ.考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
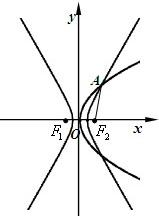 如图,抛物线C1:y2=8x与双曲线
如图,抛物线C1:y2=8x与双曲线 有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5.
有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5. ,试求所有满足条件的点P的坐标.
,试求所有满足条件的点P的坐标.
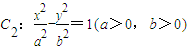 有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5.
有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5.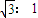 ,试求所有满足条件的点P的坐标.
,试求所有满足条件的点P的坐标.