题目内容
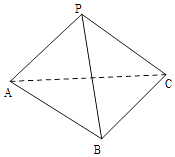
【题目】如图,四棱锥P﹣ABCD中,PD⊥底面ABCD,且底面ABCD为平行四边形,若∠DAB=60°,AB=2,AD=1. 
(1)求证:PA⊥BD;
(2)若∠PCD=45°,求点D到平面PBC的距离h.
【答案】
(1)证明:∵AD=1,AB=2,∠DAB=60°,
∴BD2=AB2+AD2﹣2ABADcos60°=3,
∴AD2+BD2=AB2,
∴AD⊥BD,
∵PD⊥平面ABCD,BD平面ABCD,
∴PD⊥BD,又AD∩PD=D,
∴BD⊥平面PAD,
∵PA平面PAD,
∴BD⊥PA
(2)解:由(1)可知BC⊥BD,
∴S△BCD= ![]() =
= ![]() ,
,
∵∠PCD=45°,∴PD=CD=2,
∴VP﹣BCD= ![]() =
= ![]() .
.
∵PC= ![]() CD=2
CD=2 ![]() ,PB=
,PB= ![]() =
= ![]() ,BC=1,
,BC=1,
∴BC2+PB2=PC2,∴PB⊥BC,
∴S△BCP= ![]() =
= ![]() ,
,
∴VD﹣BCP= ![]() =
= ![]() ,
,
又VP﹣BCD=VD﹣BCP,∴ ![]() =
= ![]() ,
,
解得h= ![]()
【解析】(1)利用勾股定理逆定理证明AD⊥BD,结合BD⊥PD得出BD⊥平面PAD,故而PA⊥BD;(2)根据VP﹣BCD=VD﹣BCP列方程解出h.
【考点精析】本题主要考查了直线与平面垂直的性质的相关知识点,需要掌握垂直于同一个平面的两条直线平行才能正确解答此题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目