题目内容
解关于
的不等式
.
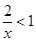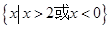
解析试题分析：该题为解分式不等式，所以关键是将其化为整式不等式求解.
试题解析：原不等式可化为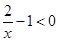
;
通分得：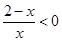
，变形为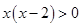
；
所以原不等式的解集为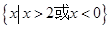
考点：分式不等式的解法.
练习册系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
小学生10分钟应用题系列答案目标测试系列答案题目内容
解关于的不等式.
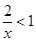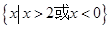
解析试题分析：该题为解分式不等式，所以关键是将其化为整式不等式求解.
试题解析：原不等式可化为;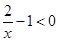
通分得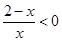：，变形为；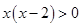
所以原不等式的解集为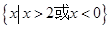
考点：分式不等式的解法.
小学生10分钟应用题系列答案目标测试系列答案
，比较f(x)与m的大小．
.
时，解不等式
；
时，
，求a的取值范围.
(k<0)的定义域为B.
，|2x－y|＜
，求证：|y|＜
.
．
的解集为
，求实数a的值； 
使
成立，求实数
的取值范围． 
，
. 
时，求不等式
的解集；
，且当
时，
，求
的取值范围。
的解为 。