题目内容
已知函数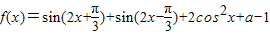 (a为常数),若函数f(x)的最大值为
(a为常数),若函数f(x)的最大值为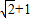 .
.(1)求实数a的值;
(2)将函数y=f(x)的图象向左平移
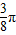 个单位,再向下平移2个单位得到函数y=g(x)的图象,求函数g(x)的单调递减区间.
个单位,再向下平移2个单位得到函数y=g(x)的图象,求函数g(x)的单调递减区间.
【答案】分析:(1)利用两角和及差的正弦对函数化简可得,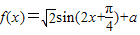 ,由
,由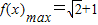 可得
可得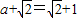 ,可求a
,可求a
(2)由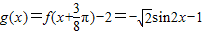 ,要求函数g(x)的单调递减区间,只要求y=sin2x的单调递增区间即可,令-
,要求函数g(x)的单调递减区间,只要求y=sin2x的单调递增区间即可,令-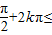 2x
2x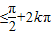 ,k∈Z可求
,k∈Z可求
解答:解:(1)∵得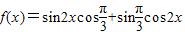 +
+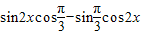 +cos2x+a
+cos2x+a
=sin2x+cos2x+a
∴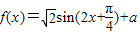 ,…(4分)
,…(4分)
由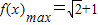 得a=1.…(3分)
得a=1.…(3分)
(2)∵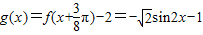 ,…(4分)
,…(4分)
令-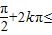 2x
2x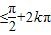 ,k∈Z
,k∈Z
∴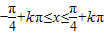 ,k∈Z
,k∈Z
∴函数的单调递减区间为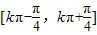 ,k∈Z.…(3分)
,k∈Z.…(3分)
点评:本题考查两角和与差的正弦公式及辅助角公式的应用,正弦函数的单调区间的求解.
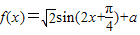 ,由
,由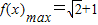 可得
可得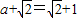 ,可求a
,可求a(2)由
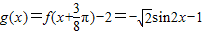 ,要求函数g(x)的单调递减区间,只要求y=sin2x的单调递增区间即可,令-
,要求函数g(x)的单调递减区间,只要求y=sin2x的单调递增区间即可,令-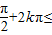 2x
2x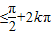 ,k∈Z可求
,k∈Z可求解答:解:(1)∵得
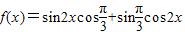 +
+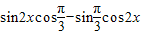 +cos2x+a
+cos2x+a=sin2x+cos2x+a
∴
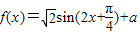 ,…(4分)
,…(4分)由
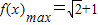 得a=1.…(3分)
得a=1.…(3分)(2)∵
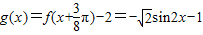 ,…(4分)
,…(4分)令-
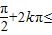 2x
2x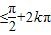 ,k∈Z
,k∈Z∴
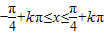 ,k∈Z
,k∈Z∴函数的单调递减区间为
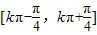 ,k∈Z.…(3分)
,k∈Z.…(3分)点评:本题考查两角和与差的正弦公式及辅助角公式的应用,正弦函数的单调区间的求解.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 ( a为常数、a∈R),
( a为常数、a∈R), .
. (a为常数)的图象经过点(1,3).
(a为常数)的图象经过点(1,3). ( a为常数、a∈R),
( a为常数、a∈R), .
. (a为常数)是R上的奇函数,函数
(a为常数)是R上的奇函数,函数
 上恒成立,求t的取值范围
上恒成立,求t的取值范围 其中a为常数,且
其中a为常数,且 .
.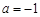 时,求
时,求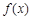 在
在 (e=2.718 28…)上的值域;
(e=2.718 28…)上的值域; 对任意
对任意 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.