题目内容
(本小题满分12分)
已知函数 其中a为常数,且
其中a为常数,且 .
.
(Ⅰ)当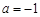 时,求
时,求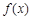 在
在 (e=2.718 28…)上的值域;
(e=2.718 28…)上的值域;
(Ⅱ)若 对任意
对任意 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】
(Ⅰ)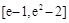
(Ⅱ)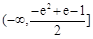
【解析】(Ⅰ)当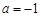 时,
时,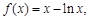
得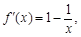 ………………………1分
………………………1分
令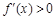 ,即
,即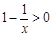 ,解得
,解得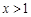 ,所以函数
,所以函数 在
在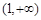 上为增函数,
上为增函数,
据此,函数 在
在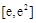 上为增函数, ………………………3分
上为增函数, ………………………3分
而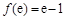 ,
,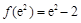 ,所以函数
,所以函数 在
在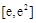 上的值域为
上的值域为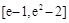
………………………4分
(Ⅱ)由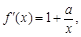 令
令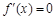 ,得
,得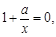 即
即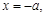
当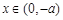 时,
时,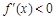 ,函数
,函数 在
在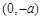 上单调递减;
上单调递减;
当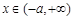 时,
时,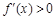 ,函数
,函数 在
在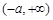 上单调递增;…………………5分
上单调递增;…………………5分
若 ,即
,即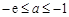 ,易得函数
,易得函数 在
在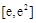 上为增函数,
上为增函数,
此时,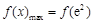 ,要使
,要使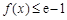 对
对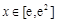 恒成立,只需
恒成立,只需 即可,
即可,
所以有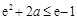 ,即
,即
而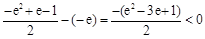 ,即
,即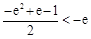 ,所以此时无解.
,所以此时无解.
………………………7分
若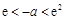 ,即
,即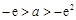 ,易知函数
,易知函数 在
在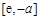 上为减函数,在
上为减函数,在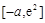 上为增函数,
上为增函数,
要使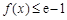 对
对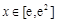 恒成立,只需
恒成立,只需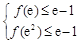 ,即
,即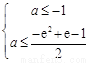 ,
,
由 和
和
得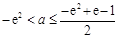 . ………………………9分
. ………………………9分
若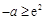 ,即
,即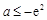 ,易得函数
,易得函数 在
在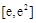 上为减函数,
上为减函数,
此时, ,要使
,要使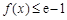 对
对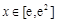 恒成立,只需
恒成立,只需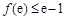 即可,
即可,
所以有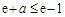 ,即
,即 ,又因为
,又因为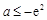 ,所以
,所以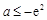 . …………………11分
. …………………11分
综合上述,实数a的取值范围是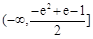 . ……………………12分
. ……………………12分

练习册系列答案
相关题目