题目内容
已知函数 ( a为常数、a∈R),
( a为常数、a∈R), .
.(1)讨论函数f(x)的单调性;
(2)当a=1时,判断函数g(x)的零点的个数,并说明理由.
【答案】分析:(1)由f(x)的解析式求出f(x)的导函数,且求出f(x)的定义域,分a大于等于0和a小于0两种情况,分别令导函数大于0列出关于x的不等式,求出不等式的解集即可得到x的范围即为函数的递增区间;令导函数小于0列出关于x的不等式,求出不等式的解集即可得到x的范围即为函数的递减区间;
(2)把a=1代入f(x)中确定出f(x)的解析式,然后把f(x)的解析式代入到g(x)中确定出g(x)的解析式,求出g(x)的导函数,分别令导函数大于0和小于0得到函数的单调区间,根据函数的增减性得到g(x)的最小值,根据最小值小于0得到函数没有零点即零点个数为0.
解答:解:(1)由f(x)= x2+alnx,得f′(x)=x+
x2+alnx,得f′(x)=x+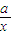 =
=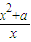 ,其中x>0.
,其中x>0.
当a≥0时,f′(x)>0对任意x∈(0,+∞)均成立,这是f(x)在区间(0,+∞)上单调递增;
当a<0时,由f′(x)>0⇒x>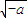 或x<-
或x<-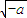 (舍)
(舍)
由f′(x)<0⇒0<x<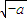 ,
,
∴f(x)在区间(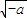 ,+∞)上单调递增,在区间(0,
,+∞)上单调递增,在区间(0,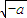 )上单调递减;
)上单调递减;
(2)a=1时,g(x)=f(x)- x3=
x3= x2+lnx-
x2+lnx- x3,
x3,
g′(x)=x+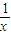 -2x2=
-2x2=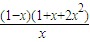 ,其中x>0,
,其中x>0,
∴x∈(0,1)时,g′(x)>0,函数g(x)单调递增;x∈(1,+∞)时,g′(x)<0,函数g(x)单调递减.
∴[g(x)]min=g(1)=- <0,
<0,
∴函数g(x)零点的个数为0.
点评:此题考查学生会根据导函数的正负得到函数的单调区间,会根据函数的增减性得到函数的最值,掌握函数零点的判断方法,是一道综合题.
(2)把a=1代入f(x)中确定出f(x)的解析式,然后把f(x)的解析式代入到g(x)中确定出g(x)的解析式,求出g(x)的导函数,分别令导函数大于0和小于0得到函数的单调区间,根据函数的增减性得到g(x)的最小值,根据最小值小于0得到函数没有零点即零点个数为0.
解答:解:(1)由f(x)=
 x2+alnx,得f′(x)=x+
x2+alnx,得f′(x)=x+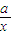 =
=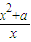 ,其中x>0.
,其中x>0.当a≥0时,f′(x)>0对任意x∈(0,+∞)均成立,这是f(x)在区间(0,+∞)上单调递增;
当a<0时,由f′(x)>0⇒x>
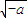 或x<-
或x<-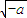 (舍)
(舍)由f′(x)<0⇒0<x<
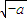 ,
,∴f(x)在区间(
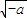 ,+∞)上单调递增,在区间(0,
,+∞)上单调递增,在区间(0,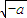 )上单调递减;
)上单调递减;(2)a=1时,g(x)=f(x)-
 x3=
x3= x2+lnx-
x2+lnx- x3,
x3,g′(x)=x+
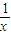 -2x2=
-2x2=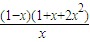 ,其中x>0,
,其中x>0,∴x∈(0,1)时,g′(x)>0,函数g(x)单调递增;x∈(1,+∞)时,g′(x)<0,函数g(x)单调递减.
∴[g(x)]min=g(1)=-
 <0,
<0,∴函数g(x)零点的个数为0.
点评:此题考查学生会根据导函数的正负得到函数的单调区间,会根据函数的增减性得到函数的最值,掌握函数零点的判断方法,是一道综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ( a为常数、a∈R),
( a为常数、a∈R), .
. (a为常数)的图象经过点(1,3).
(a为常数)的图象经过点(1,3). (a为常数)是R上的奇函数,函数
(a为常数)是R上的奇函数,函数
 上恒成立,求t的取值范围
上恒成立,求t的取值范围 其中a为常数,且
其中a为常数,且 .
.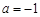 时,求
时,求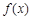 在
在 (e=2.718 28…)上的值域;
(e=2.718 28…)上的值域; 对任意
对任意 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.