题目内容
已知椭圆C: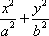 (a>b>0)的左右焦点分别是F1(-c,0),F2(c,0),直线l:x=my+c与椭圆C交于两点M,N且当m=-
(a>b>0)的左右焦点分别是F1(-c,0),F2(c,0),直线l:x=my+c与椭圆C交于两点M,N且当m=-![]() 时,M是椭圆C的上顶点,且△MF1F2的周长为6.
时,M是椭圆C的上顶点,且△MF1F2的周长为6.
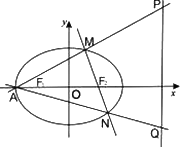
(1)求椭圆C的方程;
(2)设椭圆C的左顶点为A,直线AM,AN与直线:x=4分别相交于点P,Q,问当m变化时,以线段PQ为直径的圆被x轴截得的弦长是否为定值?若是,求出这个定值,若不是,说明理由.
答案:
解析:
解析:
|
解:(1)当 解得: 所以椭圆方程是: (1)当 又 证明如下:设点 所以点 由方程组 所以: 从而: 所以:以 |

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 3分
3分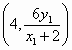 ,同理,点
,同理,点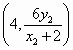 , 9分
, 9分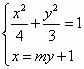 得到:
得到: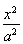









 (a>b>0)的离心率为
(a>b>0)的离心率为 ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3. (a>b>0)的离心率为
(a>b>0)的离心率为 短轴一个端点到右焦点的
短轴一个端点到右焦点的 .
. ,求△AOB面积的
,求△AOB面积的