题目内容
对于任意两个正整数m,n,定义某种运算?:当m,n都为偶数或奇数时,m?n=m+n;当m,n中一个为奇数,另一个为偶数时,m?n=m•n.则在上述定义下,集合M={(x,y)|x?y=36,x∈N*,y∈N*}中元素的个数为( )
| A、48 | B、41 | C、40 | D、39 |
考点:元素与集合关系的判断
专题:新定义
分析:根据定义,x?y=36分两类进行考虑:x和y一奇一偶,则x•y=36;x和y同奇偶,则x+y=36.由x、y∈N*列出满足条件的所有可能情况,再考虑点(x,y)的个数即可.
解答:解:x?y=36,x、y∈N*,
若x和y一奇一偶,则xy=36,满足此条件的有1×36=3×12=4×9,故点(x,y)有6个;
若x和y同奇偶,则x+y=36,满足此条件的有1+35=2+34=3+33=4+32=…=35+1,故点(x,y)有35个,
∴满足条件的个数为6+35=41个.
故选:B.
若x和y一奇一偶,则xy=36,满足此条件的有1×36=3×12=4×9,故点(x,y)有6个;
若x和y同奇偶,则x+y=36,满足此条件的有1+35=2+34=3+33=4+32=…=35+1,故点(x,y)有35个,
∴满足条件的个数为6+35=41个.
故选:B.
点评:本题为新定义问题,考查对新定义和集合的理解,正确理解新定义的含义是解决本题的关键.

练习册系列答案
相关题目
集合A,B满足A∪B={1,2},则不同的有序集合对(A,B)共有( )
| A、4个 | B、7个 | C、8个 | D、9个 |
设数集M同时满足条件①M中不含元素-1,0,1,②若a∈M,则
∈M.则下列结论正确的是( )
| 1+a |
| 1-a |
| A、集合M中至多有2个元素 |
| B、集合M中至多有3个元素 |
| C、集合M中有且仅有4个元素 |
| D、集合M中有无穷多个元素 |
下列集合中,不是方程(x+1)(x-2)(x-3)=0的解集的集合是( )
| A、{-1,2,3} | B、{3,-1,2} | C、{x|(x+1)(x-2)(x-3)=0} | D、{(-1,2,3)} |
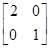 对应的变换下得到曲线F,求F的方程.
对应的变换下得到曲线F,求F的方程.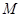 是把坐标平面上的点的横坐标伸长到3倍,纵坐标伸长到2倍的伸压变换矩阵.
是把坐标平面上的点的横坐标伸长到3倍,纵坐标伸长到2倍的伸压变换矩阵. 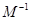 ;
;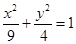 在矩阵
在矩阵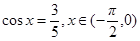 ,则
,则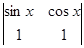 =_______
=_______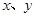 的方程组:
的方程组:
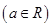 ,并对解的情况进行讨论.
,并对解的情况进行讨论.