题目内容
 给出下列三个命题:
给出下列三个命题:①函数y=
| 1 |
| 2 |
| 1-cos x |
| 1+cos x |
| x |
| 2 |
②若函数y=f(x)与y=g(x)的图象关于直线y=x对称,则函数y=f(2x)与y=
| 1 |
| 2 |
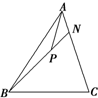
③如图,在△ABC中,
| AN |
| 1 |
| 3 |
| NC |
| AP |
| AB |
| 2 |
| 11 |
| AC |
| 3 |
| 11 |
其中真命题是( )
分析:①分别求出两个函数的定义域,利用定义域和对应法则进行判断.②根据函数关于直线y=x对称的性质进行判断.③利用向量共线的共线定理以及平面向量的定理进行判断.
解答:解:①要使函数y=
ln
有意义,则
>0,即(1+cosx)(cosx-1)<0,解得-1<cosx<1,
∴x≠kπ,k∈Z,要使y=ln tan
有意义,则tan
>0,即kπ<
<kπ+
,解得2kπ<x<2kπ+π,两个函数的定义域不同,∴不是同一函数,即①错误.
②∵函数y=f(x)与y=g(x)的图象关于直线y=x对称,∴设(x,y)是y=f(2x)上的点,则2x=g(y),即x=
g(y),即数y=f(2x)关于y=x对称函数为y=
g(x),∴②正确.
③∵
=
,
=m
+
,设
=λ
,则
=
+
=
+λ
=
+λ(
-
)=(1-λ)
+
,
∵
=m
+
,
∴m=1-λ,且
=
,解得λ=
,m=
.∴③正确.
故选:C.
| 1 |
| 2 |
| 1-cos x |
| 1+cos x |
| 1-cos x |
| 1+cos x |
∴x≠kπ,k∈Z,要使y=ln tan
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| π |
| 2 |
②∵函数y=f(x)与y=g(x)的图象关于直线y=x对称,∴设(x,y)是y=f(2x)上的点,则2x=g(y),即x=
| 1 |
| 2 |
| 1 |
| 2 |
③∵
| AN |
| 1 |
| 3 |
| NC |
| AP |
| AB |
| 2 |
| 11 |
| AC |
| BP |
| BN |
| AP |
| AB |
| BP |
| AB |
| BN |
| AB |
| AN |
| AB |
| AB |
| λ |
| 4 |
| AC |
∵
| AP |
| AB |
| 2 |
| 11 |
| AC |
∴m=1-λ,且
| λ |
| 4 |
| 2 |
| 11 |
| 8 |
| 11 |
| 3 |
| 11 |
故选:C.
点评:本题主要考查各种命题的真假判断,涉及的知识点有函数的性质,平面向量的向量分解,综合性较强.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目