题目内容
【题目】将函数![]() 的图象,向右平移
的图象,向右平移![]() 个单位长度,再把纵坐标伸长到原来的2倍,得到函数
个单位长度,再把纵坐标伸长到原来的2倍,得到函数![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 函数![]() 的最小正周期为
的最小正周期为![]() B. 函数
B. 函数![]() 在区间
在区间![]() 上单调递增
上单调递增
C. 函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() D.
D. ![]() 是函数
是函数![]() 的一条对称轴
的一条对称轴
【答案】C
【解析】
利用函数y=Asin(ωx+φ)的图象变换规律,求得f(x)的解析式,再利用正弦函数的图象和性质,判断各个选项是否正确.
将函数g(x)=2cos2(x+![]() )﹣1=cos(2x+
)﹣1=cos(2x+![]() )的图象向右平移
)的图象向右平移![]() 个单位长度,
个单位长度,
可得y=cos(2x﹣![]() +
+![]() )=cos(2x﹣
)=cos(2x﹣![]() )的图象;
)的图象;
再把纵坐标伸长到原来的2倍,得到函数f(x)=2cos(2x﹣![]() )的图象.
)的图象.
显然,f(x)的最小正周期为![]() =π,故A错误.
=π,故A错误.
在区间[![]() ]上,2x﹣
]上,2x﹣![]() ∈[π,
∈[π,![]() ],函数g(x)没有单调性,故B错误.
],函数g(x)没有单调性,故B错误.
在区间[![]() ]上,2x﹣
]上,2x﹣![]() ∈[
∈[![]() ,
,![]() ],故当2x﹣
],故当2x﹣![]() =
=![]() 时,函数f(x)取得最小值为﹣
时,函数f(x)取得最小值为﹣![]() ,故C正确.
,故C正确.
当x=![]() 时,f(x)=2cos(2x﹣
时,f(x)=2cos(2x﹣![]() )=0,不是最值,故x=
)=0,不是最值,故x=![]() 不是函数f(x)的一条对称轴,故D错误,
不是函数f(x)的一条对称轴,故D错误,
故选:C.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
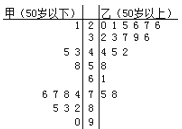
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |