题目内容
【题目】已知函数
．
（1）判断
的奇偶性与单调性；
（2）解关于
的不等式
．
【答案】（1）奇函数，增函数；（2）
.
【解析】
（1）运用奇偶性的定义和单调性的定义，即可判断；
（2）运用（1）的结论，f（x2﹣2x+2）+f（﹣5）＜0即为f（x2﹣2x+2）＜﹣f（﹣5）＝f（5），得x2﹣2x+2＜5，解出即可．
（1）∵f（﹣x）
f（x），∴f（x）是奇函数．
∵f（x）
1
，在R上任取x1，x2，且x1＜x2，
f（x1）﹣f（x2）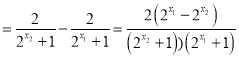
，
∵x1＜x2，∴
，
，
即有f（x1）＜f（x2），则f（x）在R上是增函数．
（2）由（1）得f（x）是奇函数，
且f（x）在R上是增函数．
则f（x2﹣2x+2）+f（﹣5）＜0即为f（x2﹣2x+2）＜﹣f（﹣5）＝f（5），
得x2﹣2x+2＜5，即有x2﹣2x﹣3＜0，
解得﹣1＜x＜3，则不等式解集为（﹣1，3）．
练习册系列答案
相关题目
