题目内容
15.(1)解$\root{3}{x+4}$+$\root{3}{3x-7}$+4x-3>0;(2)解方程$\root{3}{x+2}$+$\root{3}{2x+5}$+3x+5=0;
(3)设m=$\frac{(1+\sqrt{2001})^{2002}-(1-\sqrt{2001})^{2002}}{\sqrt{2001}}$,判断m是无理数还是有理数?并说明理由.
分析 (1)设$\root{3}{x+4}$=m,$\root{3}{3x-7}$=n,则原不等式化为:m+n+(m3+n3)=(m+n)(m2+n2-mn+1)>0,由此能求出原不等式的解集.
(2)设$\root{3}{x+2}$=m,$\root{3}{2x+5}$=n,则m+n+(m3+n3)-2=0,由此利用消元法能求出方程$\root{3}{x+2}$+$\root{3}{2x+5}$+3x+5=0的解.
(3)设$\sqrt{2001}$=a,则$\frac{(1+a)^{2002}-(1-a)^{2002}}{a}$,由此利用二项式定理能判断m是无理数还是有理数.
解答 解:(1)∵$\root{3}{x+4}$+$\root{3}{3x-7}$+4x-3>0
设$\root{3}{x+4}$=m,$\root{3}{3x-7}$=n
则原不等式化为:m+n+(m3+n3)=(m+n)(m2+n2-mn+1)>0,
又m2+n2-mn+1>0
∴不等式化为:m+n>0,
∴m3+n3=x+4+3x-7=4x-3>0,
解得x>$\frac{3}{4}$.
∴原不等式的解集为{x|x>$\frac{3}{4}$}.
(2)∵$\root{3}{x+2}$+$\root{3}{2x+5}$+3x+5=0,
设$\root{3}{x+2}$=m,$\root{3}{2x+5}$=n,
∴m+n+(m3+n3)-2=0,∴(m+n)(m2+n2-mn+1)=2,
∵m2+n2-mn+1>0,∴m+n>0,
∵m3=x+2,n3=2x+5,∴2m3+1=n3,∴m≥0,n≥1,
∴m+$\sqrt{2{m}^{3}+1}$+m3+2m3+1-2=0,
∴m=0,n=1,
∴$\left\{\begin{array}{l}{x+2=0}\\{2x+5=1}\end{array}\right.$,解得x=-2.
∴方程$\root{3}{x+2}$+$\root{3}{2x+5}$+3x+5=0的解为x=-2.
(3)设$\sqrt{2001}$=a,
则$\frac{(1+a)^{2002}-(1-a)^{2002}}{a}$
=$\frac{1}{a}{(C}_{n}^{0}{a}^{2002}-{C}_{n}^{0}{a}^{2002}+{2C}_{n}^{1}{a}^{2001}{+{C}_{n}^{n}-C}_{n}^{n})$
=${n}_{1}{a}^{2000}+{n}_{2}{a}^{1998}+…+{n}_{i}{{a}^{0}}_{\;}$,(n1,n2,…,ni都是常数),
∵$a=\sqrt{2001}$,∴a的偶数次方都是有理数,
∴m=$\frac{(1+\sqrt{2001})^{2002}-(1-\sqrt{2001})^{2002}}{\sqrt{2001}}$是有理数.
点评 本题考查不等式和方程的求解,考查有理数和无理数的判断,是中档题,解题时要注意换元法、消元法和二项式定理的合理运用.

| A. | (-$∞,\frac{3}{2}$) | B. | ($\frac{3}{2},+∞$) | C. | (-$∞,-\frac{3}{2}$) | D. | (-$\frac{3}{2},+∞$) |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分且必要条件 | D. | 既不充分又不必要条件 |
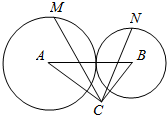 如图,圆A与圆B外切,半径分别为3,2,且△ABC是以C为直角顶点的Rt△.若AC=4.BC=3,点M,N分别在圆A,B上,则$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围是[-6-$\sqrt{145}$,6+$\sqrt{145}$].
如图,圆A与圆B外切,半径分别为3,2,且△ABC是以C为直角顶点的Rt△.若AC=4.BC=3,点M,N分别在圆A,B上,则$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围是[-6-$\sqrt{145}$,6+$\sqrt{145}$].