题目内容
3.已知等差数列{an},{bn}中的前几项和分别是Sn,Tn.若$\frac{{S}_{n}}{{T}_{n}}$=$\frac{n}{n+1}$,则$\frac{{a}_{7}}{{b}_{7}}$=$\frac{13}{14}$,$\frac{{a}_{10}}{{b}_{5}}$=$\frac{19}{10}$,$\frac{{S}_{10}}{{T}_{5}}$=$\frac{10}{3}$,$\frac{{a}_{10}}{{T}_{7}}$=$\frac{19}{56}$.分析 由等差数列的前n项和为不含常数的二次函数设出Sn,Tn,然后把要求值的分式转化为和的比值得答案.
解答 解:∵数列{an},{bn}均为等差数列,其前n项和Sn,Tn满足$\frac{{S}_{n}}{{T}_{n}}$=$\frac{n}{n+1}$,
则$\frac{{a}_{7}}{{b}_{7}}$=$\frac{13{a}_{7}}{13{b}_{7}}=\frac{{S}_{13}}{{T}_{13}}=\frac{13}{13+1}=\frac{13}{14}$;
由$\frac{{S}_{n}}{{T}_{n}}$=$\frac{n}{n+1}$,设${S}_{n}=k{n}^{2},{T}_{n}=k({n}^{2}+n)$,
则$\frac{{a}_{10}}{{b}_{5}}$=$\frac{{S}_{10}-{S}_{9}}{{T}_{5}-{T}_{4}}=\frac{19k}{10k}=\frac{19}{10}$;
$\frac{{S}_{10}}{{T}_{5}}$=$\frac{100k}{30k}=\frac{10}{3}$;
$\frac{{a}_{10}}{{T}_{7}}$=$\frac{{S}_{10}-{S}_{9}}{{T}_{7}}=\frac{19k}{56k}=\frac{19}{56}$.
故答案为:$\frac{13}{14}$;$\frac{19}{10}$;$\frac{10}{3}$;$\frac{19}{56}$.
点评 本题考查了等差数列的前n项和,考查了数学转化思想方法,是基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
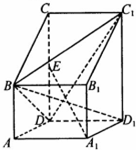 如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,AB∥CD,AD⊥CD,侧棱AA1⊥底面ABCD,E是CD的中点,CD=2AB=2AD,AD=1,AA1=$\sqrt{2}$.
如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,AB∥CD,AD⊥CD,侧棱AA1⊥底面ABCD,E是CD的中点,CD=2AB=2AD,AD=1,AA1=$\sqrt{2}$. 如图,∠ACB=90°,DA⊥平面ABC,AE⊥DB交DB于E,AF⊥DC交DC于F,且AD=AB=2,则三棱锥D-AEF体积的最大值为 $\frac{2}{9}$.
如图,∠ACB=90°,DA⊥平面ABC,AE⊥DB交DB于E,AF⊥DC交DC于F,且AD=AB=2,则三棱锥D-AEF体积的最大值为 $\frac{2}{9}$.