题目内容
5. 如图,在直棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,AB=AC=$\sqrt{2}$,AA1=3,D是BC的中点,点E在棱BB1上运动.
如图,在直棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,AB=AC=$\sqrt{2}$,AA1=3,D是BC的中点,点E在棱BB1上运动.(1)证明:AD⊥C1E
(2)当异面直线AC,C1E所成的角为$\frac{π}{3}$时,求三棱柱C1-A1B1E的体积.
分析 (1)由AB=AC=$\sqrt{2}$,D是BC的中点,可得AD⊥BC,再利用直棱柱的性质可证:AD⊥平面BCC1B1,即可得出;
(2)由AC∥A1C1,可得∠B1C1A1为异面直线AC,C1E所成的角,为$\frac{π}{3}$,利用线面垂直的判定定理可得;A1C1⊥平面A1ABB1,因此A1C1⊥A1E.利用三棱柱C1-A1B1E的体积V=$\frac{1}{3}×{S}_{△{A}_{1}{B}_{1}E}×{A}_{1}{C}_{1}$即可得出.
解答 (1)证明:如图所示,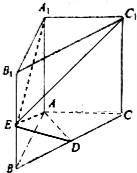
∵AB=AC=$\sqrt{2}$,D是BC的中点,
∴AD⊥BC,
∵直棱柱ABC-A1B1C1中,∴BB1⊥AD,
又BC∩BB1=B,
∴AD⊥平面BCC1B1,
∵C1E?平面BCC1B1,
∴:AD⊥C1E.
(2)解:∵AC∥A1C1,
∴∠B1C1A1为异面直线AC,C1E所成的角,为$\frac{π}{3}$,
∵A1C1⊥A1B1,AA1⊥A1C1,
A1B1∩AA1=A1,
∴A1C1⊥平面A1ABB1,
∴A1C1⊥A1E,
∴${A}_{1}E={A}_{1}{C}_{1}tan\frac{π}{3}$=$\sqrt{2}×\sqrt{3}$=$\sqrt{6}$,∴${B}_{1}E=\sqrt{{A}_{1}{E}^{2}-{A}_{1}{B}_{1}^{2}}$=2,
∴三棱柱C1-A1B1E的体积V=$\frac{1}{3}×{S}_{△{A}_{1}{B}_{1}E}×{A}_{1}{C}_{1}$=$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×2×\sqrt{2}$=$\frac{2}{3}$.
点评 本题考查了线面与垂直的判定与性质定理、直角三角形的性质、直棱柱的性质、三棱锥的体积计算公式、异面直线所成的角,考查了空间想象能力,考查了推理能力与计算能力,属于中档题.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案| A. | 5:3:4 | B. | 3:5:10 | C. | 4:3:5 | D. | 5:3:10 |
| A. | (-$\frac{1}{e}$,+∞) | B. | (-$\frac{1}{e}$,0) | C. | (-$\frac{2}{e}$,+∞) | D. | (-$\frac{2}{e}$,0) |
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
 如图1,已知四边形ABCD的对角线AC与BD互相垂直,∠A=60°,∠C=90°,CD=CB=2,将△ABD沿BD折起,得到三棱锥A′-BCD,如图2.
如图1,已知四边形ABCD的对角线AC与BD互相垂直,∠A=60°,∠C=90°,CD=CB=2,将△ABD沿BD折起,得到三棱锥A′-BCD,如图2.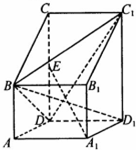 如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,AB∥CD,AD⊥CD,侧棱AA1⊥底面ABCD,E是CD的中点,CD=2AB=2AD,AD=1,AA1=$\sqrt{2}$.
如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,AB∥CD,AD⊥CD,侧棱AA1⊥底面ABCD,E是CD的中点,CD=2AB=2AD,AD=1,AA1=$\sqrt{2}$.