题目内容
8.已知四边形ABCD为圆O的内接正方形,且AB=2,EF为圆O的一条直径,M为正方形ABCD边界上一动点,∠EMF=α,α满足sin2α+cos2α=$\frac{1}{4}$,α∈($\frac{π}{2}$,π).(1)求α的大小;
(2)求△MEF的周长的取值范围.
分析 (1)利用二倍角的余弦函数公式可得cos2α=$\frac{1}{4}$,结合范围α∈($\frac{π}{2}$,π).即可得解.
(2)由余弦定理可得:8=ME2+MF2+ME×MF,①,利用基本不等式可得ME×MF≤$\frac{8}{3}$,利用平方和公式可求得:ME+MF≤$\frac{4\sqrt{6}}{3}$,又EF+ME+MF>2EF=4$\sqrt{2}$.从而可求△MEF的周长的取值范围.
解答  解:(1)∵sin2α+cos2α=sin2α+cos2α-sin2α=cos2α=$\frac{1}{4}$,
解:(1)∵sin2α+cos2α=sin2α+cos2α-sin2α=cos2α=$\frac{1}{4}$,
∴可得:cosα=±$\frac{1}{2}$,
又∵α∈($\frac{π}{2}$,π).
∴解得cosα=-$\frac{1}{2}$,α=$\frac{2π}{3}$.
(2)∵在△MEF中,由余弦定理可得:EF2=ME2+MF2-2•ME•MF•cosα,即:8=ME2+MF2+ME×MF,①,
∴由①可得:8≥2ME×MF+ME×MF=3ME×MF,解得ME×MF≤$\frac{8}{3}$,
∴由①可得:(ME+MF)2=8+ME×MF≤8+$\frac{8}{3}$=$\frac{32}{3}$.解得:ME+MF≤$\frac{4\sqrt{6}}{3}$,
∴△MEF的周长=EF+ME+MF=2$\sqrt{2}$+ME+MF≤2$\sqrt{2}$+$\frac{4\sqrt{6}}{3}$=$\frac{6\sqrt{2}+4\sqrt{6}}{3}$.
又,EF+ME+MF>2EF=4$\sqrt{2}$.
△MEF的周长的取值范围:(4$\sqrt{2}$,$\frac{6\sqrt{2}+4\sqrt{6}}{3}$].
点评 本题主要考查了二倍角的余弦函数公式的应用,考查了余弦定理,基本不等式,平方和公式的应用,考查了计算能力,属于中档题.

 天天练口算系列答案
天天练口算系列答案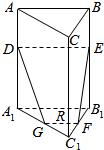 如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D、E分别在AA1、BB1上,AD=BE=1,F、G分别是B1C1、A1C1的中点,则直线GF与直线DE的距离为( )
如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D、E分别在AA1、BB1上,AD=BE=1,F、G分别是B1C1、A1C1的中点,则直线GF与直线DE的距离为( )| A. | $\sqrt{3}$ | B. | $\frac{3\sqrt{6}}{4}$ | C. | $\frac{2\sqrt{5}}{3}$ | D. | $\frac{\sqrt{19}}{2}$ |
| A. | $\frac{2\sqrt{34}}{17}$ | B. | $\frac{3\sqrt{17}}{17}$ | C. | -$\frac{2\sqrt{34}}{17}$ | D. | -$\frac{3\sqrt{17}}{17}$ |
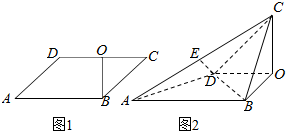 如图1,平行四边形ABCD中,AB=2,BC=$\sqrt{2}$,∠BAD=45°,O为CD中点,将△BOC沿OB边翻折,折成直二面角A-BO-C,E为AC中点,
如图1,平行四边形ABCD中,AB=2,BC=$\sqrt{2}$,∠BAD=45°,O为CD中点,将△BOC沿OB边翻折,折成直二面角A-BO-C,E为AC中点,