题目内容
16.已知函数f(x)=2x,x1,x2是任意实数,且x1≠x2,证明$\frac{1}{2}$[f(x1)+f(x2)]>f($\frac{{x}_{1}{+x}_{2}}{2}$)分析 根据基本不等式得$\frac{1}{2}$[${2}^{{x}_{1}}$+${2}^{{x}_{2}}$]≥$\frac{1}{2}$•2•$\sqrt{{2}^{{x}_{1}+{x}_{2}}}$=${2}^{\frac{{x}_{1}+{x}_{2}}{2}}$,这是证明本命题的关键.
解答 证明:因为函数f(x)=2x,x1,x2是任意实数,所以,
左边=$\frac{1}{2}$[f(x1)+f(x2)]=$\frac{1}{2}$[${2}^{{x}_{1}}$+${2}^{{x}_{2}}$],
右边=f($\frac{{x}_{1}{+x}_{2}}{2}$)=${2}^{\frac{{x}_{1}+{x}_{2}}{2}}$,
根据基本不等式,
$\frac{1}{2}$[${2}^{{x}_{1}}$+${2}^{{x}_{2}}$]≥$\frac{1}{2}$•2•$\sqrt{{2}^{{x}_{1}+{x}_{2}}}$=${2}^{\frac{{x}_{1}+{x}_{2}}{2}}$,
由于x1≠x2,所以,$\frac{1}{2}$[${2}^{{x}_{1}}$+${2}^{{x}_{2}}$]>${2}^{\frac{{x}_{1}+{x}_{2}}{2}}$,
因此,左边>右边,
即:$\frac{1}{2}$[f(x1)+f(x2)]>f($\frac{{x}_{1}{+x}_{2}}{2}$).
点评 本题主要考查了运用基本等式证明不等式问题,涉及到函数值的计算,和取等条件的分析,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
1.三棱锥P-ABC三条侧棱两两垂直,PA=a,PB=b,PC=c,三角形ABC的面积为S,则顶点P到底面的距离是( )
| A. | $\frac{abc}{6s}$ | B. | $\frac{abc}{3s}$ | C. | $\frac{abc}{2s}$ | D. | $\frac{abc}{s}$ |
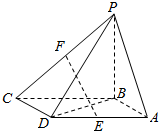 如图所示,四棱锥P ABCD的底面ABCD是平行四边形,BA=BD=$\sqrt{2}$,AD=2,PA=PD=$\sqrt{5}$,E,F分别是棱AD,PC的中点,二面角PADB为60°.
如图所示,四棱锥P ABCD的底面ABCD是平行四边形,BA=BD=$\sqrt{2}$,AD=2,PA=PD=$\sqrt{5}$,E,F分别是棱AD,PC的中点,二面角PADB为60°. 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点.