题目内容
【题目】已知A,B是焦距为![]() 的椭圆
的椭圆![]()
![]() 的上、下顶点,P是椭圆上异于顶点的任意一点,直线PA,PB的斜率之积为
的上、下顶点,P是椭圆上异于顶点的任意一点,直线PA,PB的斜率之积为![]() .
.
(1)求椭圆的方程;
(2)若C,D分别是椭圆的左、右顶点,动点M满足![]() ,连接CM交椭圆于点E,试问:x轴上是否存在定点T,使得
,连接CM交椭圆于点E,试问:x轴上是否存在定点T,使得![]() 恒成立?若存在,求出点T坐标,若不存在,请说明理由.
恒成立?若存在,求出点T坐标,若不存在,请说明理由.
【答案】(1)![]() (2)存在定点
(2)存在定点![]() 满足题意
满足题意
【解析】
(1)设![]() ,代入椭圆方程可得
,代入椭圆方程可得![]() ,由
,由![]()
![]()
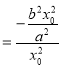
![]()
![]() ,则
,则![]() ,又由
,又由![]() ,进而求得
,进而求得![]() ,从而求得椭圆方程;
,从而求得椭圆方程;
(2)设![]() ,法一:设
,法一:设![]()
![]() ,由C,E,M共线得
,由C,E,M共线得![]() ,则
,则![]() ,由E在椭圆上,可得
,由E在椭圆上,可得![]() ,代入
,代入![]() 中求解即可;
中求解即可;
法二:设直线![]() ,则
,则![]() ,联立
,联立 可得
可得![]() ,则
,则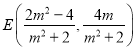 ,代入
,代入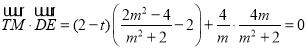 中求解即可
中求解即可
(1)由题,![]()
![]() ,设
,设![]() ,
,
则![]() ,所以
,所以![]() ,
,
所以![]()
![]()
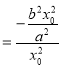
![]()
![]() ,
,
所以![]() ,
,
又![]()
![]() ,
,
所以![]()
![]() ,
,
所以椭圆的方程为![]()
(2)存在,
设其坐标为![]() ,由题,
,由题,![]()
![]() ,
,
法一:设![]()
![]() ,
,
由C,E,M共线得![]() ,即
,即![]() ,所以
,所以![]() ,
,
由E在椭圆上,得![]() ,则
,则![]() ,
,
因为![]() ,
,![]() ,
,
所以![]()
![]()
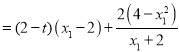
![]() 恒成立,
恒成立,
所以![]() ,即存在定点
,即存在定点![]() 满足题意
满足题意
法二:设直线![]() ,其中
,其中![]() ,
,
令![]() 得
得![]() ,
,
联立 ,
,
得![]() ,
,
故![]() ,所以
,所以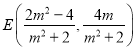 ,
,
所以![]() ,
, ,
,
故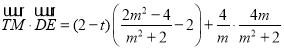
![]() 恒成立,
恒成立,
所以![]() ,即存在定点
,即存在定点![]() 满足题意
满足题意

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目