已知$f(x)=\left\{\begin{array}{l}{log 3}x.x＞0\\{2^{-x}}.x≤0\end{array}\right.$.则$f+f({log 2}^{\frac{1}{6}})$=( )A．$-\frac{11}{6}$B．-8C．4D．8 题目和参考答案——青夏教育精英家教网—

题目内容

14．已知$f（x）=\left\{\begin{array}{l}{log_3}x，x＞0\\{2^{-x}}，x≤0\end{array}\right.$，则$f（\frac{1}{9}）+f（{log_2}^{\frac{1}{6}}）$=（　　）

A．

$-\frac{11}{6}$

B．

-8

C．

D．

分析直接利用否定函数求解函数值即可．

解答解：$f（x）=\left\{\begin{array}{l}{log_3}x，x＞0\\{2^{-x}}，x≤0\end{array}\right.$，
则$f（\frac{1}{9}）+f（{log_2}^{\frac{1}{6}}）$=log₃$\frac{1}{9}$+${2}^{{-log}_{2}\frac{1}{6}}$=-2+6=4．
故选：C．

点评本题考查分段函数的解析式的应用，函数值的求法，考查计算能力．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

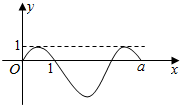
$\frac{{\sqrt{3}}}{2}$

D．

-3

5．在△ABC中，内角A，B，C的对边分别为a，b，c，向量$\overrightarrow m=（cos（A-B），sin（A-B））$，$\overrightarrow n=（cosB，-sinB）$，且$\overrightarrow m•\overrightarrow n=-\frac{3}{5}$．
（Ⅰ）求sinA的值；
（Ⅱ）若$a=4\sqrt{2}，b=5$，求$\overrightarrow{AB}•\overrightarrow{BC}$的值．

2．函数f（x）=log${\;}_{\frac{1}{2}}$（2x-x²）的单调递减区间为（　　）

9．已知函数f（x）=log_ax（a＞0且a≠1），且函数的图象过点（2，1）．
（1）求函数f（x）的解析式；
（2）若f（m²-m）＜1成立，求实数m的取值范围．

19．已知各项均为正数的数列{a_n}的前n项和为S_n，满足$a_{n+1}^2=2{S_n}+n+4，且{a_2}-1，{a_3}，{a_7}$恰为等比数列{b_n}的前3项．
（1）求数列{a_n}，{b_n}的通项公式；
（2）若${c_n}={b_n}+\frac{1}{{{a_n}{a_{n+1}}}}$，求数列{c_n}的前n项和T_n．

6．已知$\overrightarrow{AB}$、$\overrightarrow{AC}$是非零向量且满足（$\overrightarrow{AB}-$2$\overrightarrow{AC}$）⊥$\overrightarrow{AB}$，（$\overrightarrow{AC}$-2$\overrightarrow{AB}$）$⊥\overrightarrow{AC}$，则∠A等于（　　）

3．数列{a_n}满足a_na_n+1-a_n+1=-1，a₂₀₁₆=-1，则a₃₆₁等于（　　）

4．利用更相减损之术求1230与411的最大公约数，第三次做差所得差值为3．

试题分类