题目内容
(本小题满分12分)
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组 ;第二组
;第二组 ……第五组
……第五组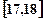 .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图. 
(I)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(II)设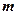 、
、 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知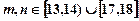 .
.
求事件“ ”的概率.
”的概率.
解:(1)由直方图知,
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
成绩在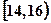 内的人数为:
内的人数为: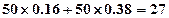 (人)
(人)
所以该班成绩良好的人数为27人. -----4分
(2)由直方图知,成绩在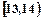 的人数为
的人数为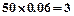 人,设为
人,设为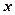 、
、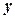 、
、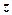 ;-----5分
;-----5分
成绩在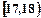 的人数为
的人数为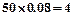 人,设为
人,设为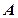 、
、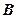 、
、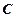 、
、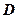 .-----6分
.-----6分
若 时,有
时,有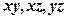 共3种情况;-----7分
共3种情况;-----7分
若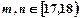 时,有
时,有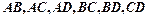 共6种情况;-----8分
共6种情况;-----8分
若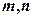 分别在
分别在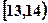 和
和 内时,
内时,
共有12种情况. -----10分 A B C D x xA xB xC xD y yA yB yC yD z zA zB zC zD
所以基本事件总数为21种,事件“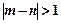 ”所包含的基本事件个数有12种.
”所包含的基本事件个数有12种.
∴P(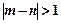 )=
)=解析

(13分)
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2)求出y关于x的线性回归方程;
(3)试预测加工10个零件需要多长时间?
某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2) 试预测加工10个零件需要多少时间?

(本题12分)
在测量一根新弹簧的劲度系数时,测得了如下的结果:
所挂重量(N)( ) ) | 1 | 2 | 3 | 5 | 7 |  9 9 |
| 弹簧长度(cm)(y) | 11 | 12 | 12 | 13 | 14 | 16 |

(1)请画出上表所给数据的散点图;
(2)弹簧长度与所挂重量之间的关系是否具有线性相关性,若具有请根据上表提供的数据,求出y关于x的线性回归方程
 =bx+a;
=bx+a;(3)根据回归方程,求挂重量为8N的物体时弹簧的长度.所求的长度是弹簧的实际长度吗?为什么?
(本小题满分12分)高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
 | ① | ② |
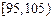 | | 0.050 |
 | | 0.200 |
 | 12 | 0.300 |
 | | 0.275 |
 | 4 | ③ |
 | | 0.050 |
| 合 计 | | ④ |
 、③、④处的数值分别是多少?
、③、④处的数值分别是多少?(2)在坐标系中画出
 的频率分布直方图;
的频率分布直方图;(3)根据题中信息估计总体平均数,并估计总体落在
 中的概率。
中的概率。 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2) 请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 ;
;(3) 已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考数据: 3×2.5+4×3+5×4+6×4.5=66.5)
(本小题满分12分)品厂为了检查甲、乙两条自动包装流水线的生产情况,在这两条
流水线上各抽取40件产品作为样本称 出它们的重量(单位:克),重量值落在(495,510]
出它们的重量(单位:克),重量值落在(495,510]
的产 品为合格品,否则为不合格品,表1是甲流水线样本频数分布表,
品为合格品,否则为不合格品,表1是甲流水线样本频数分布表, 图1是乙流水线样
图1是乙流水线样
本的频率分布直方图。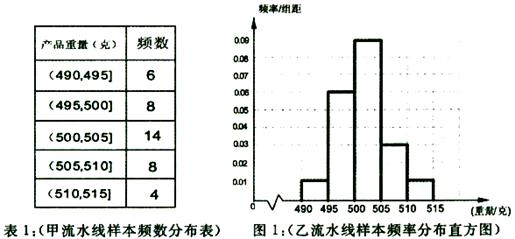 某食
某食
(1)若检验员不小心将甲、乙两条流水线生产的重量值在(510,515]的产品放在了一起,
然后又随机取出3件产品,求至少有一件是乙流水线生产的产品的概率;
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为“产品的包装质量
与两条自动包装流水线的选择有关”。
| | 甲流水线 | 乙流水线 | 合 计 |
| 合格品 | a= | b= | |
| 不合格品 | c= | d= | |
| 合 计 | | | n= |
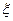 ,求
,求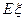 .
.
 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出