题目内容
(本小题满分12分)
第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行 ,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”。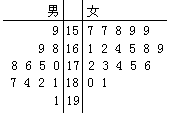
(1)如果用分层抽样的方法从“高个子”和“非高个子”中中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用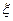 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出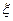 的分布列,并求
的分布列,并求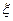 的数学期望。
的数学期望。
解:(1)根据茎叶图,有“高个子”12人,“非高个子”18人,…………………………1分
用分层抽样的方法,每个人被抽中的概率是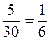 , …………………………2分
, …………………………2分
所以选中的“高个子”有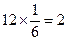 人,“非高个子”有
人,“非高个子”有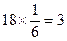 人.…………………3分
人.…………………3分
用事件 表示“至少有一名“高个子”被选中”,则它的对立事件
表示“至少有一名“高个子”被选中”,则它的对立事件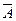 表示“没有一名“高个子”被选中”,
表示“没有一名“高个子”被选中”,
则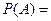
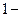
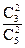
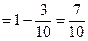 . ………………………………5分
. ………………………………5分
因此,至少有一人是“高个子”的概率是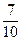 . ……………………………6分
. ……………………………6分
(2)依题意,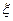 的取值为
的取值为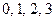 . ……………………………7分
. ……………………………7分
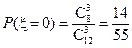 ,
, 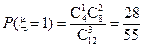 ,
,
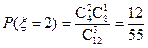 ,
, 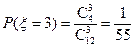 . ………………………9分
. ………………………9分
因此,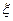 的分布列如下:
的分布列如下:
………………10分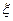
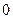
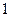
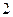
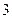
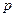
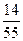
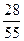
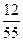
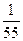
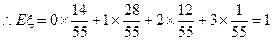 . …………………………12分
. …………………………12分
解析

(本小题满分12分)
某中学共有1000名学生参加了该地区高三第一次质量检测的数学考试,数学成绩如下表所示:
| 数学成绩分组 | 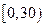 |  |  | 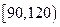 |  |
| 人数 | 60 | 90 | 300 | x | 160 |
样的方法抽取100名同学进行问卷调查,甲同学在本次测试中数学成绩为95分,
求他被抽中的概率;
(II)已知本次数学成绩的优秀线为110分,试根据所提供数据估计该中学达到优秀线的人数;
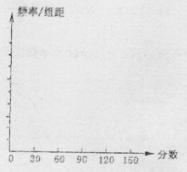
(III)作出频率分布直方图,并估计该学校本次考试的数学平均分。(同一组中的数据用该组区间的中点值作代表)
(本小题满分12分)
某校为了探索一种新的教学模式,进行了一项课题实验,乙班为实验班,甲班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,成绩如下表(总分:150分):
甲班
| 成绩 | 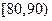 | 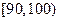 |  | 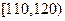 | 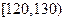 |
| 频数 | 4 | 20 | 15 | 10 | 1 |
| 成绩 | 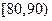 | 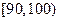 |  | 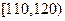 | 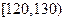 |
| 频数 | 1 | 11 | 23 | 13 | 2 |
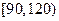 内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;(Ⅱ)根据所给数据可估计在这次测试中,甲班的平均分是101.8,请你估计乙班的平均分,并计算两班平均分相差几分;
(Ⅲ)完成下面2×2列联表,你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由。
| | 成绩小于100分[来源:学科网ZXXK] | 成绩不小于100分 | 合计 |
| 甲班 | 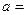 | 26 | 50 |
| 乙班 | 12 | 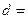 | 50 |
| 合计 | 36 | 64 | 100 |
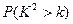 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
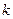 | 2.072 | 2.706 | 3.841[来源:Z.xx.k.Com] | 5.024 | 6.635 | 7.879 | 10.828 |
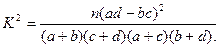
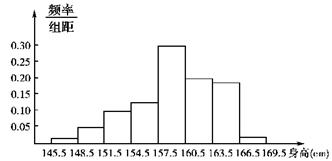
 表1:男生身高频数分布表
表1:男生身高频数分布表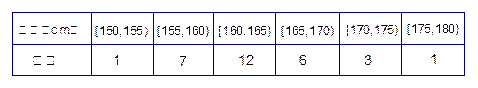 表2:女生身高频数分布表
表2:女生身高频数分布表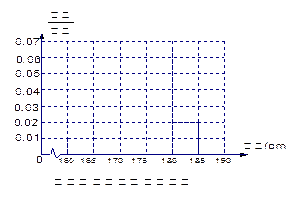
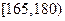 的概率;
的概率; 的男生中任选3人,设
的男生中任选3人,设 表示所选3人中身高(单位:cm)在
表示所选3人中身高(单位:cm)在 的人数,求
的人数,求 的频率;(2)根据频率分布直方图算出样本数据的
的频率;(2)根据频率分布直方图算出样本数据的 的这段应抽多少人?
的这段应抽多少人?
 ;第二组
;第二组 ……第五组
……第五组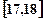 .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图. 
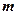 、
、 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知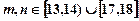 .
. ”的概率.
”的概率.