题目内容
已知椭圆 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
(1)求过点O、F,并且与椭圆的左准线l相切的圆的方程;
(2)设过点F且不与坐标轴垂直交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围。
(2)设过点F且不与坐标轴垂直交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围。
解:(1))∵a2=2,b2=1,
∴c=1,F(-1,0),l:x=-2
∵圆过点O、F,
∴圆心M在直线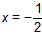 上
上
设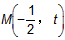
则圆半径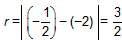
由|OM|=r,得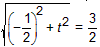
解得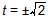
∴所求圆的方程为 。
。
(2)设直线AB的方程为y=k(x+1)(k≠0),
代入 ,整理得(1+2k2)x2+4k2x+2k2-2=0
,整理得(1+2k2)x2+4k2x+2k2-2=0
∵直线AB过椭圆的左焦点F,
∴方程有两个不等实根
记A(x1,y1),B(x2,y2),AB中点N(x0,y0),则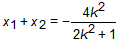
∴AB的垂直平分线NG的方程为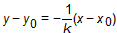
令y=0,得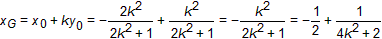
∵k≠0
∴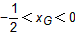
∴点G横坐标的取值范围为 。
。
∴c=1,F(-1,0),l:x=-2
∵圆过点O、F,
∴圆心M在直线
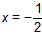 上
上设
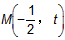
则圆半径
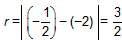
由|OM|=r,得
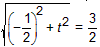
解得
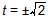
∴所求圆的方程为
 。
。(2)设直线AB的方程为y=k(x+1)(k≠0),
代入
 ,整理得(1+2k2)x2+4k2x+2k2-2=0
,整理得(1+2k2)x2+4k2x+2k2-2=0∵直线AB过椭圆的左焦点F,
∴方程有两个不等实根
记A(x1,y1),B(x2,y2),AB中点N(x0,y0),则
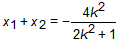
∴AB的垂直平分线NG的方程为
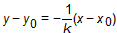
令y=0,得
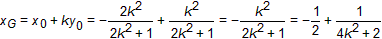
∵k≠0
∴
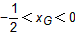
∴点G横坐标的取值范围为
 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的左焦点为F,O为坐标原点.
的左焦点为F,O为坐标原点.
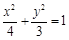 的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
 ,求直线AB的斜率;
,求直线AB的斜率; 的左焦点为F,左右顶点分别为A、C,
的左焦点为F,左右顶点分别为A、C, ,其中圆心P的坐标为
,其中圆心P的坐标为 .
. ,求
,求 上,求椭圆的方程.
上,求椭圆的方程. 的左焦点为F,右顶点为A,点B在椭圆上,且
的左焦点为F,右顶点为A,点B在椭圆上,且 轴,直线AB交
轴,直线AB交 轴于点P。若
轴于点P。若 ,则椭圆的离心率为
,则椭圆的离心率为