题目内容
已知椭圆 的左焦点为F,O为坐标原点.
的左焦点为F,O为坐标原点.(I)求过点O、F,并且与椭圆的左准线l相切的圆的方程;
(II)设过点F的直线交椭圆于A、B两点,并且线段AB的中点在直线x+y=0上,求直线AB的方程.

【答案】分析:(I)由题意可知圆过点O(0,0)、F(-1,0),圆心M在直线 上.由此可求出圆的方程.
上.由此可求出圆的方程.
(II)设直线AB的方程为y=k(x+1)(k≠0),代入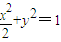 ,整理得(1+2k2)x2+4k2x+2k2-2=0.然后利用根与系数的关系进行求解.
,整理得(1+2k2)x2+4k2x+2k2-2=0.然后利用根与系数的关系进行求解.
解答: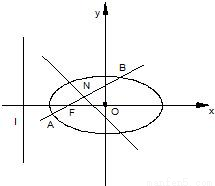 解:(I)∵a2=2,b2=1,
解:(I)∵a2=2,b2=1,
∴c=1,F(-1,0),l:x=-2.
∵圆过点O、F,
∴圆心M在直线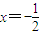 上.
上.
设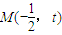 ,则圆半径
,则圆半径
由|OM|=r,得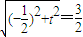 ,
,
解得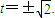
∴所求圆的方程为
(II)设直线AB的方程为y=k(x+1)(k≠0),
代入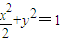 ,整理得(1+2k2)x2+4k2x+2k2-2=0.
,整理得(1+2k2)x2+4k2x+2k2-2=0.
∵直线AB过椭圆的左焦点F,
∴方程有两个不等实根,
记A(x1,y1),B(x2,y2),AB中点N(x,y),
则 ,
,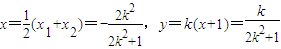 ,
,
∵线段AB的中点N在直线x+y=0上,
∴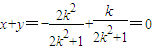 ,
,
∴k=0,或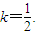
当直线AB与x轴垂直时,线段AB的中点F不在直线x+y=0上.
∴直线AB的方程是y=0,或x-2y+1=0.
点评:本题主要考查直线、圆、椭圆和不等式等基本知识,考查平面解析几何的基本方法,考查运算能力和综合解题能力.解题时要注意公式的灵活运用.
 上.由此可求出圆的方程.
上.由此可求出圆的方程.(II)设直线AB的方程为y=k(x+1)(k≠0),代入
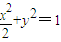 ,整理得(1+2k2)x2+4k2x+2k2-2=0.然后利用根与系数的关系进行求解.
,整理得(1+2k2)x2+4k2x+2k2-2=0.然后利用根与系数的关系进行求解.解答:
 解:(I)∵a2=2,b2=1,
解:(I)∵a2=2,b2=1,∴c=1,F(-1,0),l:x=-2.
∵圆过点O、F,
∴圆心M在直线
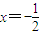 上.
上.设
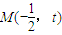 ,则圆半径
,则圆半径
由|OM|=r,得
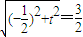 ,
,解得
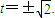
∴所求圆的方程为

(II)设直线AB的方程为y=k(x+1)(k≠0),
代入
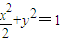 ,整理得(1+2k2)x2+4k2x+2k2-2=0.
,整理得(1+2k2)x2+4k2x+2k2-2=0.∵直线AB过椭圆的左焦点F,
∴方程有两个不等实根,
记A(x1,y1),B(x2,y2),AB中点N(x,y),
则
 ,
,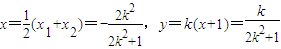 ,
,∵线段AB的中点N在直线x+y=0上,
∴
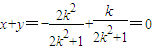 ,
,∴k=0,或
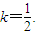
当直线AB与x轴垂直时,线段AB的中点F不在直线x+y=0上.
∴直线AB的方程是y=0,或x-2y+1=0.
点评:本题主要考查直线、圆、椭圆和不等式等基本知识,考查平面解析几何的基本方法,考查运算能力和综合解题能力.解题时要注意公式的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
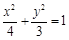 的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
 ,求直线AB的斜率;
,求直线AB的斜率; 的左焦点为F,左右顶点分别为A、C,
的左焦点为F,左右顶点分别为A、C, ,其中圆心P的坐标为
,其中圆心P的坐标为 .
. ,求
,求 上,求椭圆的方程.
上,求椭圆的方程. 的左焦点为F,右顶点为A,点B在椭圆上,且
的左焦点为F,右顶点为A,点B在椭圆上,且 轴,直线AB交
轴,直线AB交 轴于点P。若
轴于点P。若 ,则椭圆的离心率为
,则椭圆的离心率为