题目内容
如图,已知椭圆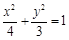 的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.

(Ⅰ)若点G的横坐标为 ,求直线AB的斜率;
,求直线AB的斜率;
(Ⅱ)记△GFD的面积为S1,△OED(O为原点)的面积为S2.
试问:是否存在直线AB,使得S1=S2?说明理由.
【答案】
(Ⅰ)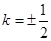 .
.
(Ⅱ)不存在直线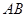 ,使得
,使得 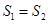 . 12分
. 12分
【解析】
试题分析:(Ⅰ)依题意,直线 的斜率存在,设其方程为
的斜率存在,设其方程为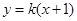 .
.
将其代入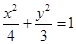 ,
,
整理得 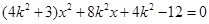 .
.
设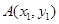 ,
,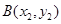 , 所以
, 所以
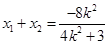 .
4分
.
4分
故点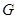 的横坐标为
的横坐标为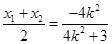 .
.
依题意,得 ,
,
解得 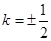 . 6分
. 6分
(Ⅱ)解:假设存在直线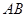 ,使得
,使得 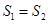 ,显然直线
,显然直线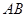 不能与
不能与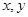 轴垂直.
轴垂直.

由(Ⅰ)可得
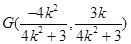 .
.
因为 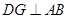 ,所以
,所以 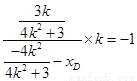 ,
,
解得 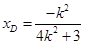 ,
即
,
即 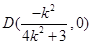 .
.
因为 △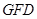 ∽△
∽△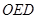 ,
,
所以  .
.
所以  ,
,
整理得 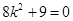 .
.
因为此方程无解,所以不存在直线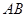 ,使得
,使得 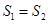 . 12分
. 12分
考点:本题主要考查椭圆的标准方程,直线与椭圆的位置关系,三角形面积计算。
点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(2)利用弦长公式,确定得到三角形面积表达式,实现对“存在性问题”的研究。

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
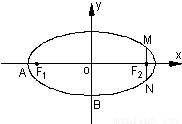
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:


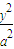 +
+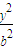 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=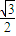 ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的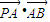 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.