题目内容
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,E为PA的中点,F为BC的中点,底面ABCD是菱形,对角线AC,BD交于点O.求证: 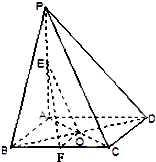
(1)平面EFO∥平面PCD;
(2)平面PAC⊥平面PBD.
【答案】
(1)解:因为E为PA的中点,O为AC的中点,所以EO∥PC
又EO平面PCD,PC平面PCD,所以EO∥平面PCD
同理可证,FO∥平面PCD,又EO∩FO=O
所以,平面EFO∥平面PCD
(2)解:因为PA⊥平面ABCD,BD平面ABCD,所以PA⊥BD
因为底面ABCD是菱形,所以AC⊥BD,又PA∩AC=A
所以BD⊥平面PAC
又BD平面PBD,所以平面PAC⊥平面PBD
【解析】(1)由题意知,EO∥PC,由线面平行的判定定理得到EO∥平面PCD,同理可证,FO∥平面PCD,再由面面平行的判定定理,即得证平面EFO∥平面PCD.(2)由于PA⊥平面ABCD,得到PA⊥BD,再由已知得到BD⊥平面PAC,由面面垂直的判定定理,即得证平面PAC⊥平面PBD.
【考点精析】关于本题考查的平面与平面平行的判定和平面与平面垂直的判定,需要了解判断两平面平行的方法有三种:用定义;判定定理;垂直于同一条直线的两个平面平行;一个平面过另一个平面的垂线,则这两个平面垂直才能得出正确答案.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目