题目内容
16．已知z（2-i）=11+7i，若|z1|=1，则|z-z1|的最大值为$\sqrt{34}+1$．分析 根据复数的基本运算以及复数的模长公式以及复数的几何意义进行求解即可．
解答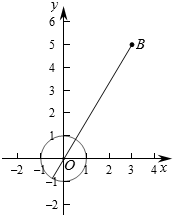 
解：由z（2-i）=11+7i得z=$\frac{11+7i}{2-i}$=$\frac{（11+7i）（2+i）}{（2-i）（2+i）}$=$\frac{15+25i}{5}$=3+5i，
则|z-z1|=|z1-z|=|z1-（3+5i）|，
∵|z1|=1，
∴|z1-（3+5i）|的几何意义为单位圆上的点到点B（3，5）的距离，
作出对应的图象如图：
则|z-z1|的最大值为|OB|+1=$\sqrt{{3}^{2}+{5}^{2}}$+1=$\sqrt{34}+1$，
故答案为：$\sqrt{34}+1$．
点评 本题主要考查复数的基本运算和复数的几何意义，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
6．函数f（x）=3+xlnx的单调递减区间是（ ）
| A． | （$\frac{1}{e}$，e） | B． | （0，$\frac{1}{e}$） | C． | （-∞，$\frac{1}{e}$） | D． | （$\frac{1}{e}$，+∞） |
4．在平行四边形ABCD中，AC与BD相交于点O，E是线段OD中点，AE的延长线交DC于点F，若$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AD}=\overrightarrow b$，则$\overrightarrow{AF}$=（ ）
| A． | $\frac{1}{3}\overrightarrow a+\overrightarrow b$ | B． | $\frac{1}{2}\overrightarrow a+\overrightarrow b$ | C． | $\overrightarrow a+\frac{1}{3}$$\overrightarrow b$ | D． | $\overrightarrow a+\frac{1}{2}\overrightarrow b$ |
