题目内容
下列命题中:
①若p,q为两个命题,则“p且q为真”是“p或q为真”的必要不充分条件.
②若p为:?×∈R,x2+2x≤0,则?p为:?×∈R,x2+2x>0.
③命题“?x,x2-2x+3>0”的否命题是“?x,x2-2x+3<0”.
④命题“若?p,则q”的逆否命题是“若p,则?q”.
其中正确结论的个数是( )
①若p,q为两个命题,则“p且q为真”是“p或q为真”的必要不充分条件.
②若p为:?×∈R,x2+2x≤0,则?p为:?×∈R,x2+2x>0.
③命题“?x,x2-2x+3>0”的否命题是“?x,x2-2x+3<0”.
④命题“若?p,则q”的逆否命题是“若p,则?q”.
其中正确结论的个数是( )
分析:根据复合命题的真值表判断出命题①错误;据含量词的命题的否定判断出命题②对,命题③是错误.根据四种命题的形式判断出命题④错误.
解答:解:对于①p且q为真?p为真且q为真,p或q为真?p为真或q为真,
∴“p且q为真”⇒“p或q为真”,但反之不成立,
∴“p且q为真”是“p或q为真”的充分不必要条件,故①错;
对于②,∵命题p:?×∈R,x2+2x≤0是特称命题
∴?p:?×∈R,x2+2x>0.故②正确;
③:∵“?x,x2-2x+3>0”是全称命题,它的否定命题是特称命题,即:?p为“?x,x2-2x+3≤0.
而③中给出的命题“?x,x2-2x+3>0”的否定是“?x,x2-2x+3<0”,不是否命题.故③错误;
对于④,由于逆否命题是把原命题的否命题了的结论作条件、否定了的条件作结论得到的命题,故④不正确;
其中正确结论的是②.
故选A.
∴“p且q为真”⇒“p或q为真”,但反之不成立,
∴“p且q为真”是“p或q为真”的充分不必要条件,故①错;
对于②,∵命题p:?×∈R,x2+2x≤0是特称命题
∴?p:?×∈R,x2+2x>0.故②正确;
③:∵“?x,x2-2x+3>0”是全称命题,它的否定命题是特称命题,即:?p为“?x,x2-2x+3≤0.
而③中给出的命题“?x,x2-2x+3>0”的否定是“?x,x2-2x+3<0”,不是否命题.故③错误;
对于④,由于逆否命题是把原命题的否命题了的结论作条件、否定了的条件作结论得到的命题,故④不正确;
其中正确结论的是②.
故选A.
点评:本小题主要考查复合命题的真假、四种命题的真假关系、全称命题与特称命题的相互转化问题等基础知识,这里注意全称命题的否定为特称命题,反过来特称命题的否定是全称命题.属于基础题.

练习册系列答案
相关题目
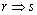 B.p:
B.p: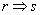 q:
q: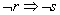
 q:
q:  D. p:
D. p: q:
q: