题目内容
下列命题中错误的个数是( )
①命题“若x2-3x+2=0,则x=1”的否命题是“若x2-3x+2=0,则x≠1”
②命题P:?x0∈R,使sinx0>1,则¬P:?x0∈R,使sinx0≤1
③若P且q为假命题,则P、q均为假命题
④“φ=
+2kπ(k∈Z)”是函数y=sin(2x+φ)为偶函数的充要条件.
①命题“若x2-3x+2=0,则x=1”的否命题是“若x2-3x+2=0,则x≠1”
②命题P:?x0∈R,使sinx0>1,则¬P:?x0∈R,使sinx0≤1
③若P且q为假命题,则P、q均为假命题
④“φ=
| π |
| 2 |
分析:根据否命题的定义,写出原命题的否命题,可判断①的真假;
根据特殊命题的否定方法,求出原命题的否定形式,可判断②的真假;
根据复合命题真假判断的真值表,可知当P且q为假命题时,不一定P、q均为假命题,可判断③的真假;
根据正弦型函数的对称性,分析出函数y=sin(2x+φ)为偶函数的充要条件,进而判断④的真假;
根据特殊命题的否定方法,求出原命题的否定形式,可判断②的真假;
根据复合命题真假判断的真值表,可知当P且q为假命题时,不一定P、q均为假命题,可判断③的真假;
根据正弦型函数的对称性,分析出函数y=sin(2x+φ)为偶函数的充要条件,进而判断④的真假;
解答:解:命题“若x2-3x+2=0,则x=1”的否命题是“若x2-3x+2≠0,则x≠1”,故①错误;
命题P:?x0∈R,使sinx0>1,则¬P:?x0∈R,使sinx0≤1,故②正确;
若P且q为假命题,则P与q至少存在一个假命题,可能是一真一假,不一定P、q均为假命题,故③错误;
当“φ=
+2kπ(k∈Z)”时函数y=sin(2x+φ)为偶函数,但函数y=sin(2x+φ)为偶函数时,“φ=
+kπ(k∈Z)”,故“φ=
+2kπ(k∈Z)”是函数y=sin(2x+φ)为偶函数的充分不必要条件,故④错误;
故选C
命题P:?x0∈R,使sinx0>1,则¬P:?x0∈R,使sinx0≤1,故②正确;
若P且q为假命题,则P与q至少存在一个假命题,可能是一真一假,不一定P、q均为假命题,故③错误;
当“φ=
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故选C
点评:本题考查的知识点是命题的真假判断,四种命题,特称命题与全称命题的否定,复合命题,充要条件,正弦型函数的单调性,难度不大.

练习册系列答案
相关题目
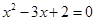 则x=1”的否命题是“若
则x=1”的否命题是“若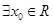 ,使
,使 ,则
,则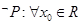 ,使
,使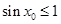
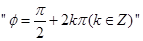 是函数
是函数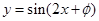 为偶函数的充要条件
为偶函数的充要条件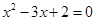 ,则
,则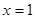 ”的否命题是“若
”的否命题是“若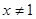 ”
”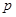 :
: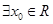 ,使
,使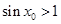 ,则
,则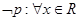 ,使
,使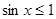
 为假命题,则
为假命题,则 是函数
是函数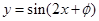 为偶函数的充要条件
为偶函数的充要条件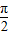 +2kπ(k∈Z)”是函数y=sin(2x+φ)为偶函数的充要条件.
+2kπ(k∈Z)”是函数y=sin(2x+φ)为偶函数的充要条件.