题目内容
1．若函数f（x+1）=x2-2x+1，求函数f（x）的单调区间．分析 先求出函数f（x）的解析式，结合一元二次函数的单调性进行求解即可．
解答 解：设t=x+1，则x=t-1，
∵f（x+1）=x2-2x+1，
∴f（t）=（t-1）2-2（t-1）+1=t2-4t+4=（t-2）2，
即f（x）=（x-2）2，对称轴为x=2，
则函数的单调递增区间为为[2，+∞），单调递减区间为为（-∞，2]．
点评 本题主要考查函数单调区间的求解，利用换元法求出函数的解析式，结合一元二次函数的单调性是解决本题的关键．
练习册系列答案
相关题目
12．设A={递增等比数列的公比}，B={递减等比数列的公比}，则A∪B=（ ）
| A． | （-∞，+∞） | B． | （1，+∞） | C． | （0，1）∪（1，+∞） | D． | ∅ |
13．在△ABC中，若BC=2，sinA=$\frac{2\sqrt{2}}{3}$，则$\overrightarrow{AB}$•$\overrightarrow{AC}$的最大值为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{4}{5}$ | C． | 1 | D． | 3 |
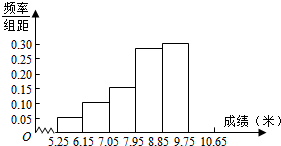某市为了解今年高中毕业生的体能状况，从本市某校高中毕业班中抽取一个班进行铅球测试，成绩在8.0米（精确到0.1米）以上的为合格．把所得数据进行整理后，分成6组画出频率分布直方图的一部分（如图），已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30，第6小组的频数是7．