Question

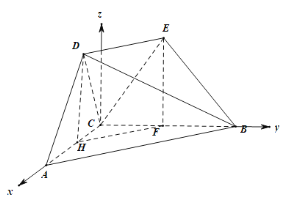
【题目】如图,在多面体ABCDE中,DE∥AB,AC⊥BC,BC＝2AC＝2,AB＝2DE,且D点在平面ABC内的正投影为AC的中点H且DH＝1．

（1）证明：面BCE⊥面ABC

（2）求BD与面CDE夹角的余弦值．

Answer 1

【答案】（1）证明见解析（2）．

【解析】

（1）证明：取BC的中点F,连接EF,HF．证明四边形DEFH为平行四边形．然后证明DH⊥平面ABC,即可证明面ECB⊥面ABC．

（2）以C为原点,建立空间直角坐标系,求出平面CDE的法向量,求出,然后通过空间向量的数量积求解即可．

（1）证明：取BC的中点F,连接EF,HF．

∵H,F分别为AC,BC的中点,

∴HF∥AB,且AB＝2HF．

又DE∥AB,AB＝2DE,

∴HF∥DE且HF＝DE,

∴四边形DEFH为平行四边形．

∴EF∥DH,

又D点在平面ABC内的正投影为AC的中点H,

∴DH⊥平面ABC,

∴EF⊥平面ABC,

∵EF面BCE

∴面ECB⊥面ABC．

（2）解：∵DH⊥平面ABC,AC⊥BC,

∴以C为原点,建立空间直角坐标系,

则B（0,2,0）,D（,0,1）,E（0,1,1）

设平面CDE的法向（x,y,z）,（,0,1）,（0,1,1）,

则,取y＝1,则x＝2,z＝﹣1．

∴,

∵,设BD与面CDE夹角为,

∴,

∴BD与面CDE夹角的余弦值为 ．