题目内容
(Ⅰ)已知|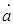 |=4,|
|=4,|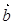 |=3,(2
|=3,(2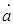 -3
-3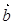 )·(2
)·(2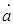 +
+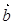 )=61,求
)=61,求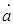 与
与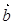 的夹角θ;
的夹角θ;
(Ⅱ)设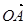 =(2,5),
=(2,5),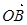 =(3,1),
=(3,1),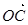 =(6,3),在
=(6,3),在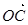 上是否存在点M,使
上是否存在点M,使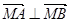 ,若存在,求出点M的坐标,若不存在,请说明理由.
,若存在,求出点M的坐标,若不存在,请说明理由.
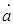 |=4,|
|=4,|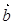 |=3,(2
|=3,(2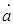 -3
-3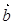 )·(2
)·(2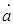 +
+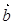 )=61,求
)=61,求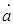 与
与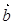 的夹角θ;
的夹角θ;(Ⅱ)设
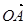 =(2,5),
=(2,5),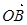 =(3,1),
=(3,1),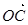 =(6,3),在
=(6,3),在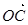 上是否存在点M,使
上是否存在点M,使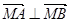 ,若存在,求出点M的坐标,若不存在,请说明理由.
,若存在,求出点M的坐标,若不存在,请说明理由.(Ⅰ)∵(2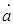 -3
-3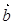 )·(2
)·(2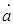 +
+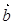 )=61,∴
)=61,∴ …(2分)
…(2分)
又|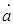 |=4,|
|=4,|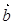 |=3,∴
|=3,∴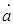 ·
·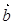 =-6.…………………………………(4分).
=-6.…………………………………(4分).
 ………………………………………………(5分)
………………………………………………(5分)
∴θ=120°.………………………………………………………(6分)
(Ⅱ)设存在点M,且

 …………………………(8分)
…………………………(8分)

∴存在M(2,1)或 满足题意.
满足题意.
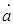 -3
-3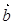 )·(2
)·(2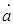 +
+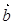 )=61,∴
)=61,∴ …(2分)
…(2分)又|
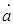 |=4,|
|=4,|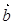 |=3,∴
|=3,∴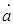 ·
·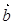 =-6.…………………………………(4分).
=-6.…………………………………(4分). ………………………………………………(5分)
………………………………………………(5分)∴θ=120°.………………………………………………………(6分)
(Ⅱ)设存在点M,且


 …………………………(8分)
…………………………(8分)
∴存在M(2,1)或
 满足题意.
满足题意.(1)根据向量的运算性质,先求出向量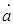 与
与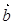 的数量积,再利用夹角公式求角。
的数量积,再利用夹角公式求角。
(2)根据向量共线的条件先把点M的坐标用点C的坐标表示出来,然后根据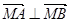 建立议程。看关于
建立议程。看关于 的方程是否有解,来判断是否存在点M的坐标。
的方程是否有解,来判断是否存在点M的坐标。
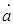 与
与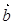 的数量积,再利用夹角公式求角。
的数量积,再利用夹角公式求角。(2)根据向量共线的条件先把点M的坐标用点C的坐标表示出来,然后根据
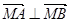 建立议程。看关于
建立议程。看关于 的方程是否有解,来判断是否存在点M的坐标。
的方程是否有解,来判断是否存在点M的坐标。
练习册系列答案
相关题目
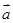 =(
=(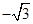 ,1),
,1),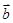 =(
=(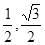 ),
),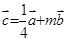 ,
,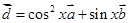 ,
,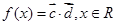 .
. 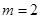 时,求
时,求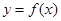 的取值范围;
的取值范围; 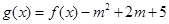 ,是否存在实数
,是否存在实数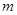 ,使得
,使得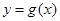 有最大值2,若存在,求出所有满足条件的
有最大值2,若存在,求出所有满足条件的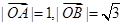 ,
,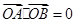 点
点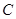 在
在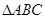 内,且
内,且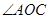
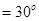 。设
。设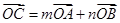
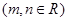 ,则
,则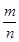 等于
等于


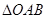 是以
是以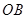 为斜边的等腰直角三角形,若
为斜边的等腰直角三角形,若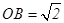 ,
,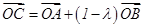 且
且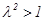 ,则
,则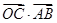 的取值范围是( )
的取值范围是( )



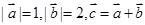 ,且
,且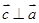 ,则向量
,则向量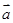 与
与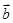 的夹角为( )
的夹角为( ) 的夹角为
的夹角为 ,
, ,则向量
,则向量 的模( )
的模( ) 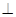 AB,
AB,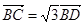 ,
,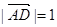 ,则
,则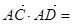 _________.
_________.