题目内容
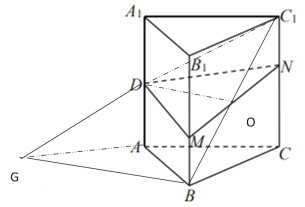
【题目】正三棱柱![]() (底面是正三角形,侧棱垂直底面)的各条棱长均相等,
(底面是正三角形,侧棱垂直底面)的各条棱长均相等,![]() 为
为![]() 的中点.
的中点.![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的动点(含端点),且满足
上的动点(含端点),且满足![]() .当
.当![]() 运动时,下列结论中正确的是______ (填上所有正确命题的序号).
运动时,下列结论中正确的是______ (填上所有正确命题的序号).

①平面![]() 平面
平面![]() ;
;
②三棱锥![]() 的体积为定值;
的体积为定值;
③![]() 可能为直角三角形;
可能为直角三角形;
④平面![]() 与平面
与平面![]() 所成的锐二面角范围为
所成的锐二面角范围为![]() .
.
【答案】①②④
【解析】
由![]() ,得到线段
,得到线段![]() 一定过正方形
一定过正方形![]() 的中心
的中心![]() ,由
,由![]() 平面
平面![]() ,可得平面
,可得平面![]() 平面
平面![]() ;
;
由![]() 的面积不变,
的面积不变,![]() 到平面
到平面![]() 的距离不变,可得三棱锥
的距离不变,可得三棱锥![]() 的体积为定值;
的体积为定值;
利用反证法思想说明![]() 不可能为直角三角形;
不可能为直角三角形;
平面![]() 与平面平行时所成角为0,当
与平面平行时所成角为0,当![]() 与
与![]() 重合,
重合,![]() 与
与![]() 重合,平面
重合,平面![]() 与平面
与平面![]() 所成的锐二面角最大.
所成的锐二面角最大.
如图:
当![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的动点(含端点),且满足
上的动点(含端点),且满足![]() ,则线段
,则线段![]() 一定过正方形
一定过正方形![]() 的中心
的中心![]() ,而
,而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,可得平面
,可得平面![]() 平面
平面![]() ,故①正确;
,故①正确;
当![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的动点(含端点),过点
上的动点(含端点),过点![]() 作
作![]() 边上的高的长等于
边上的高的长等于![]() 的长,所以
的长,所以![]() 的面积不变,由于
的面积不变,由于![]() 平面
平面![]() ,故点
,故点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,则点
的距离,则点![]() 到平面
到平面![]() 的距离为定值,故三棱锥
的距离为定值,故三棱锥![]() 的体积为定值;所以②正确;
的体积为定值;所以②正确;
由![]() 可得:
可得:![]() ,若
,若![]() 为直角三角形,则一定是以
为直角三角形,则一定是以![]() 为直角的直角三角形,但
为直角的直角三角形,但![]() 的最大值为
的最大值为![]() ,而此时
,而此时![]() ,
,![]() 的长都大于
的长都大于![]() ,故
,故![]() 不可能为直角三角形,所以③不正确;
不可能为直角三角形,所以③不正确;
当![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,平面
的中点,平面![]() 与平面
与平面![]() 平行,所成角为0;
平行,所成角为0;
当![]() 与
与![]() 重合,
重合,![]() 与
与![]() 重合,平面
重合,平面![]() 与平面
与平面![]() 所成锐二面角最大;
所成锐二面角最大;
延长![]() 角
角![]() 于
于![]() ,连接
,连接![]() ,则平面
,则平面![]() 平面
平面![]() ,由于
,由于![]() 为
为![]() 的中点,
的中点,![]() ,所以
,所以![]() ,且
,且![]() ,故在
,故在![]() 中,
中,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点,
中点,
在![]() 中,
中,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点,故
中点,故![]() ,由于
,由于![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,则
,则![]() ,
,![]() , 所以平面
, 所以平面![]() 与平面
与平面![]() 所成锐二面角最大为
所成锐二面角最大为![]() ,故④正确;
,故④正确;
故答案为①②④

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各随机抽取了100件产品作为样本来检测一项质量指标值,若产品的该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表1是甲套设备的样本的频数分布表,图是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲套设备的样本的频数分布表,图是乙套设备的样本的频率分布直方图.

表甲套设备的样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 2 | 10 | 36 | 38 | 12 | 2 |
(1)将频率视为概率.若乙套设备生产了10000件产品,则其中的合格品约有多少件?
(2)填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.01的前提下,认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附表及公式: ,其中
,其中![]() ;
;
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 20 | 40 | 80 | 50 | 10 | |
男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 45 | 75 | 90 | 60 | 30 |
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的波动大小(不计算具体值,给出结论即可);

(2)把评分不低于70分的用户称为“评分良好用户”,能否有![]() 的把握认为“评分良好用户”与性别有关?
的把握认为“评分良好用户”与性别有关?
参考附表:
|
|
|
|
|
|
|
|
|
|
参考公式 ,其中
,其中![]()

