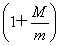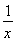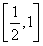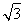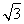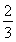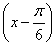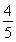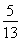Question

若sinα＝，sinβ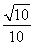＝，且α、β均为锐角，求α＋β的值．

 

Answer 1

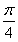
【解析】学生错【解析】

【解析】
∵α为锐角，∴cosα＝.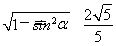

又β为锐角，∴cosβ＝.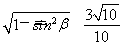

∵sin(α＋β)＝sinαcosβ＋cosαsinβ＝，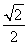

由于0°<α<90°，0°<β<90°，

∴0°<α＋β<180°，故α＋β＝45°或135°.

审题引导：在已知值求角中，角的范围常常被忽略或不能发现隐含的角的大小关系而出现增根不能排除．要避免上述情况的发生，应合理选择三角函数形式进行求解，根据计算结果，估算出角的较精确的取值范围，并不断缩小角的范围，在选择三角函数公式时，一般已知正切函数值，选正切函数，已知正余弦函数值时，若角在(0，π)时，一般选余弦函数，若是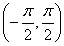，则一般选正弦函数．

规范解答：【解析】
∵α为锐角，∴cosα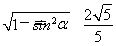＝.(2分)

又β为锐角，∴cosβ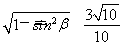＝.(4分)

且cos(α＋β)＝cosαcosβ－sinαsinβ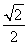＝，(10分)

由于0<α<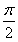，0<β<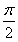，所以0<α＋β<π，

因为y＝cosx在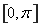上是单调递减函数，故α＋β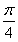＝.(14分)

错因分析：没有注意挖掘题目中的隐含条件，忽视了对角的范围的限制，造成出错．

事实上，仅由sin(α＋β)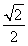＝，0°<α＋β<180°而得到α＋β＝45°或135°是正确的，但题设中sinα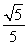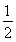＝<，sinβ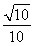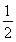＝<，使得0°<α<30°，0°<β<30°从而0°<α＋β<60°，故上述结论是错误的．在已知值求角中，应合理选择三角函数形式进行求解，避免增根．本题中0<α＋β<π，因为y＝cosx在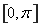上是单调函数，所以本题先求cos(α＋β)不易出错．