题目内容
已知函数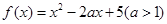 .
.
(1)若 的定义域和值域均是
的定义域和值域均是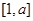 ,求实数
,求实数 的值;
的值;
(2)若 在区间
在区间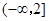 上是减函数,且对任意的
上是减函数,且对任意的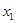 ,
,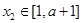 ,总有
,总有 ,求实数
,求实数 的取值范围.
的取值范围.
(1)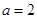 ;(2)
;(2) 的取值范围是
的取值范围是 .
.
解析试题分析:(1)根据条件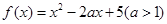 ,可知
,可知 为二次函数,其对称轴为
为二次函数,其对称轴为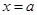 ,因此
,因此 在
在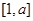 上是减函数,故根据条件
上是减函数,故根据条件 的定义域和值域均是
的定义域和值域均是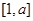 ,可列出关于
,可列出关于 的方程组
的方程组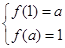 ,将
,将 具体的表达式代入,即可求得
具体的表达式代入,即可求得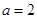 ;(2)首先根据条件可知
;(2)首先根据条件可知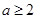 ,再由问题的描述,可将问题等价转化为求使对任意的
,再由问题的描述,可将问题等价转化为求使对任意的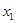 ,
,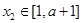 ,总有
,总有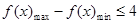 成立的
成立的 的取值范围,又由条件,二次函数
的取值范围,又由条件,二次函数 的对称轴
的对称轴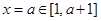 ,且左右端点
,且左右端点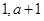 对于对称轴
对于对称轴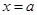 的偏离距离
的偏离距离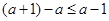 ,故有
,故有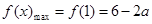 ,
,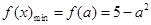 ,因此可以建立关于
,因此可以建立关于 的不等式,从而求得
的不等式,从而求得 的取值范围是
的取值范围是 .
.
试题解析:(1)∵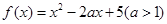 ,∴
,∴ 在
在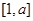 上是减函数 2分,
上是减函数 2分,
又定义域和值域均为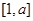 ,∴
,∴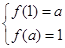 , 4分
, 4分
即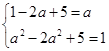 ,解得
,解得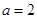 . 5分;
. 5分;
(2)∵ 在区间
在区间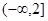 上是减函数,∴
上是减函数,∴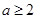 , 7分
, 7分
又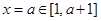 ,且
,且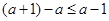 ,
,
∴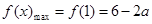 ,
,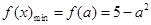 . 10分
. 10分
∵对任意的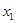 ,
,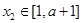 ,总有
,总有 ,
,
∴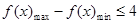 , 12分
, 12分
即 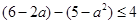 ,解得
,解得 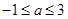 ,
,
又∵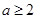 ,∴
,∴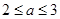 ,
, 的取值范围是
的取值范围是 .
.
考点:1.二次函数的值域;2.二次函数与恒成立问题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
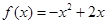 .
.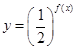 的最小值;
的最小值;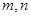 ,当
,当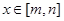 时,
时,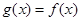 ,且
,且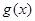 的值域为
的值域为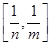 ?若存在,求出所有的
?若存在,求出所有的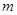 (单位:万元)的关系有经验公式
(单位:万元)的关系有经验公式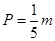 ,
, 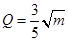 . 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资
. 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资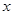 (单位:万元)
(单位:万元)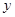 (单位:万元)关于
(单位:万元)关于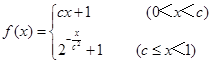 ,且
,且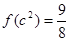 .
.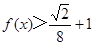 .
.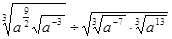 ;
;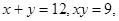 且
且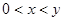 ,求
,求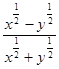 的值.
的值. .
.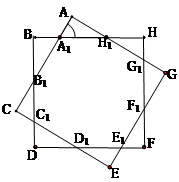
 表示
表示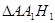 的面积;
的面积; 是定义在
是定义在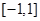 上的奇函数,且
上的奇函数,且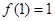 ,若
,若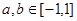 ,
,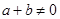 有
有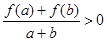 恒成立.
恒成立.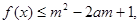 对所有
对所有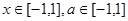 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.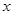 (单位:cm)满足关系:
(单位:cm)满足关系: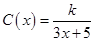 (
(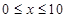 ,
,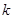 为常数),若不建隔热层,每年能源消耗费用为8万元.设
为常数),若不建隔热层,每年能源消耗费用为8万元.设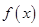 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.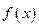 在
在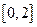 内单调递减,若
内单调递减,若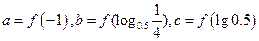 ,则
,则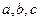 之间的大小关系为 。
之间的大小关系为 。