题目内容
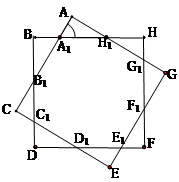
如图,制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形.由对称性,图中8个三角形都是全等的三角形,设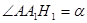 .
.
(1)试用 表示
表示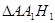 的面积;
的面积;
(2)求八角形所覆盖面积的最大值,并指出此时 的大小.
的大小.
(1)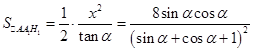 ,
,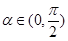
(2)八角形所覆盖面积的最大值为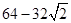 ,
,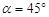
解析试题分析:探索性情景问题中的条件探索型问题,一般利用函数思想建模,由题意设出未知量,找到对应的等量关系是解决问题的关键所在,故对于(1)设出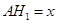 则
则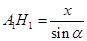 ,
,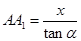 ;由
;由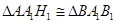 可得
可得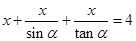 ;对于(2)换元法是解题常用方法,可以减少许多不必要的运算量,提高解题效率,注意换元前后的对等关系,令
;对于(2)换元法是解题常用方法,可以减少许多不必要的运算量,提高解题效率,注意换元前后的对等关系,令 代入面积表达式可得:
代入面积表达式可得: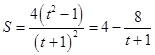 .
.
(1)设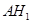 为
为 ,∴
,∴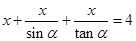 ,
,  ,
,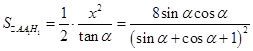 ,
,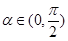 ,
,
(2)令 ,
,
只需考虑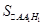 取到最大值的情况,即为
取到最大值的情况,即为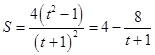 ,
,
当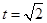 , 即
, 即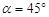 时,
时, 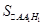 达到最大
达到最大
此时八角形所覆盖面积的最大值为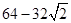 .
.
考点:函数建模和函数最值.

练习册系列答案
相关题目
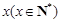 名员工从事第三产业,调整后他们平均每人每年创造利为
名员工从事第三产业,调整后他们平均每人每年创造利为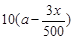 万元
万元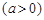 ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高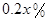 .
.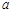 的取值范围是多少?
的取值范围是多少?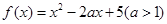 .
. 的定义域和值域均是
的定义域和值域均是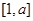 ,求实数
,求实数 的值;
的值;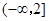 上是减函数,且对任意的
上是减函数,且对任意的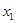 ,
,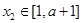 ,总有
,总有 ,求实数
,求实数 是
是 上的奇函数,且当
上的奇函数,且当 时,
时, .
.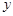 (千辆/时)与汽车的平均速度
(千辆/时)与汽车的平均速度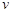 (千米/时)之间的函数关系为
(千米/时)之间的函数关系为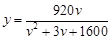 (
(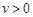 ).
).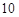 千辆/时,则汽车的平均速度应在什么范围内?
千辆/时,则汽车的平均速度应在什么范围内?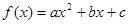 (a≠0)满足
(a≠0)满足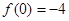 ,
,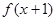 为偶函数,且x=-2是函数
为偶函数,且x=-2是函数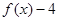 的一个零点.又
的一个零点.又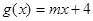 (
( >0).
>0).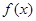 的解析式;
的解析式;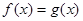 在
在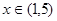 上有解,求实数
上有解,求实数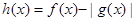 ,求
,求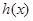 的单调区间.
的单调区间.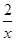 且f(4)=
且f(4)=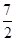 .
.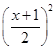 .
.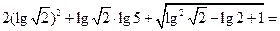
 __________.
__________.