题目内容
设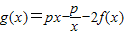 ,其中f(x)=lnx.
,其中f(x)=lnx.(Ⅰ)若g(x)在其定义域内为增函数,求实数p的取值范围;
(Ⅱ)证明:f(x)≤x-1;
(Ⅲ)证明:
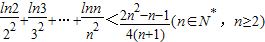 .
.
【答案】分析:(Ⅰ)要使g(x)在(0,+∞)为增函数,它的导数大于0即可,即 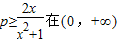 上恒成立,利用
上恒成立,利用
基本不等式求出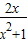 的最大值,p应大于或等于此最大值.
的最大值,p应大于或等于此最大值.
(Ⅱ)只要证明k(x)=lnx-x+1≤0即可,利用它的导数求出函数k(x)的最大值为0,可以得出结论.
(Ⅲ)因为 lnx≤x-1,又x>0,换元可得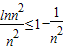 ,即
,即 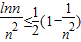 ,利用此不等式
,利用此不等式
化简要证的不等式的左边,再用放缩法可证它小于不等式的右边.
解答:解:(Ⅰ)∵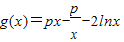 (x>0),
(x>0),
∴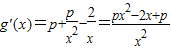 .(1分)
.(1分)
令h(x)=px2-2x+p,要使g(x)在(0,+∞)为增函数,
只需h(x)在(0,+∞)上满足:h(x)≥0恒成立,
即px2-2x+p≥0.即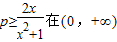 上恒成立.
上恒成立.
又∵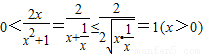 ,(4分)
,(4分)
∴p≥1.(5分)
(Ⅱ)证明:要证lnx≤x-1,
即证lnx-x+1≤0(x>0),
设k(x)=lnx-x+1,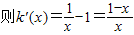 .(6分)
.(6分)
当x∈(0,1]时,k'(x)>0,∴k(x)为单调递增函数;
当x∈(1,+∞)时,k'(x)<0,∴k(x)为单调递减函数;
∴k(x)max=k(1)=0.(9分)
即lnx-x+1≤0,∴lnx≤x-1.(10分)
(Ⅲ)由(Ⅱ)知lnx≤x-1,又x>0,
∴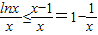 .
.
∵n∈N*,n≥2,可令x=n2,得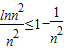 .(12分)
.(12分)
∴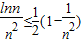 .
.
∴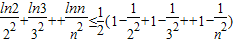 =
=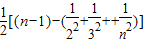
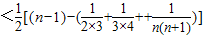
=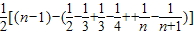
=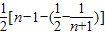 =
=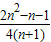 .(14分)
.(14分)
点评:本题考查利用函数的导数判断函数的单调性、求函数的最值,以及利用放缩法证明不等式.
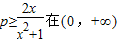 上恒成立,利用
上恒成立,利用基本不等式求出
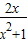 的最大值,p应大于或等于此最大值.
的最大值,p应大于或等于此最大值.(Ⅱ)只要证明k(x)=lnx-x+1≤0即可,利用它的导数求出函数k(x)的最大值为0,可以得出结论.
(Ⅲ)因为 lnx≤x-1,又x>0,换元可得
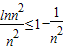 ,即
,即 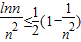 ,利用此不等式
,利用此不等式化简要证的不等式的左边,再用放缩法可证它小于不等式的右边.
解答:解:(Ⅰ)∵
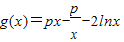 (x>0),
(x>0),∴
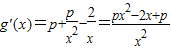 .(1分)
.(1分)令h(x)=px2-2x+p,要使g(x)在(0,+∞)为增函数,
只需h(x)在(0,+∞)上满足:h(x)≥0恒成立,
即px2-2x+p≥0.即
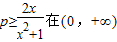 上恒成立.
上恒成立.又∵
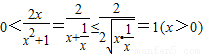 ,(4分)
,(4分)∴p≥1.(5分)
(Ⅱ)证明:要证lnx≤x-1,
即证lnx-x+1≤0(x>0),
设k(x)=lnx-x+1,
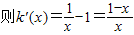 .(6分)
.(6分)当x∈(0,1]时,k'(x)>0,∴k(x)为单调递增函数;
当x∈(1,+∞)时,k'(x)<0,∴k(x)为单调递减函数;
∴k(x)max=k(1)=0.(9分)
即lnx-x+1≤0,∴lnx≤x-1.(10分)
(Ⅲ)由(Ⅱ)知lnx≤x-1,又x>0,
∴
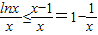 .
.∵n∈N*,n≥2,可令x=n2,得
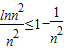 .(12分)
.(12分)∴
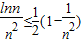 .
.∴
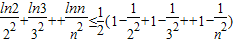 =
=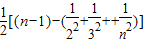
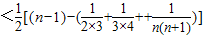
=
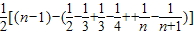
=
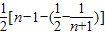 =
=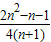 .(14分)
.(14分)点评:本题考查利用函数的导数判断函数的单调性、求函数的最值,以及利用放缩法证明不等式.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 ,其中e为自然对数的底数.
,其中e为自然对数的底数.