题目内容
给出下列命题:
①半径为2,圆心角的弧度数为
的扇形的周长为5;
②若向量
∥
且
∥
,则
∥
③设f(x)=asin(πx+α)+bcos(πx+β),其中a,b,α,β∈R,且ab≠0,α≠kπ (k∈Z).则f(2012)+f(2013)=0.
④若直线l过点A(2,3),且垂直于向量a=(2,1),则其方程为2x+y-7=0
其中真命题的序号是
①半径为2,圆心角的弧度数为
| 1 |
| 2 |
②若向量
| a |
| b |
| b |
| c |
| a |
| c |
③设f(x)=asin(πx+α)+bcos(πx+β),其中a,b,α,β∈R,且ab≠0,α≠kπ (k∈Z).则f(2012)+f(2013)=0.
④若直线l过点A(2,3),且垂直于向量a=(2,1),则其方程为2x+y-7=0
其中真命题的序号是
①③④
①③④
.分析:①由弧长公式可求得半径为2,圆心角的弧度数为
的扇形的弧长,可判断①的正误;
②若
=
,可判断②的正误;
③利用正弦函数与余弦函数的周期性可判断③;
④利用直线的点斜式方程可求得直线l的方程,从而可判断④的正误.
| 1 |
| 2 |
②若
| b |
| 0 |
③利用正弦函数与余弦函数的周期性可判断③;
④利用直线的点斜式方程可求得直线l的方程,从而可判断④的正误.
解答:解:①依题意,由弧长公式l=θr=2×
=1,
∴半径为2,圆心角的弧度数为
的扇形的周长为2+2+1=5,①正确;
对于②,当
=
时,向量
∥
且
∥
,则不能⇒
∥
,故②错误;
③∵f(x)=asin(πx+α)+bcos(πx+β),
∴f(2012)+f(2013)
=asin(2012π+α)+bcos(2012π+β)+asin(2013π+α)+bcos(2013π+β)
=asinα+bcosβ-asinα-bcosβ=0,故③正确;
④∵直线l过点A(2,3),且垂直于向量a=(2,1),
∴直线l的斜率为-2,由点斜式得直线l的方程为:y-3=-2(x-2),整理得2x+y-7=0.故④正确.
∴真命题的序号是①③④.
故答案为:①③④.
| 1 |
| 2 |
∴半径为2,圆心角的弧度数为
| 1 |
| 2 |
对于②,当
| b |
| 0 |
| a |
| b |
| b |
| c |
| a |
| c |
③∵f(x)=asin(πx+α)+bcos(πx+β),
∴f(2012)+f(2013)
=asin(2012π+α)+bcos(2012π+β)+asin(2013π+α)+bcos(2013π+β)
=asinα+bcosβ-asinα-bcosβ=0,故③正确;
④∵直线l过点A(2,3),且垂直于向量a=(2,1),
∴直线l的斜率为-2,由点斜式得直线l的方程为:y-3=-2(x-2),整理得2x+y-7=0.故④正确.
∴真命题的序号是①③④.
故答案为:①③④.
点评:本题考查命题的真假判断与应用,考查弧长公式、向量的性质、三角函数的周期性及直线的点斜式方程,属于中档题.

练习册系列答案
相关题目
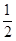 的扇形面积为
的扇形面积为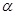 、
、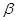 为锐角,
为锐角,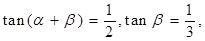 则
则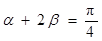 ;
;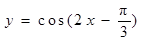 的一条对称轴是
的一条对称轴是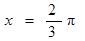 ;
;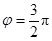 是函数
是函数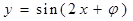 为偶函数的一个充分不必要条件.
为偶函数的一个充分不必要条件. 的扇形面积为
的扇形面积为 ;
; ,tan β=
,tan β= ,则α+2β=
,则α+2β=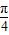 ;
;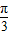 )的一条对称轴是x=
)的一条对称轴是x=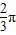 ;
;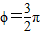 是函数y=sin(2x+ϕ)为偶函数的一个充分不必要条件.
是函数y=sin(2x+ϕ)为偶函数的一个充分不必要条件.